근의공식 뜻
예시로 제시한 수식인 x²+4x+4=0에서 근의공식을 적용하면 x = -2가 나오는데, 이는 이차방정식 x²+4x+4의 해인 x=-2를 구하는 공식이다.
일반적인 이차방정식은 ax²+bx+c=0의 형태를 가지며, 이를 풀기 위해서는 근의공식이 필요하다. 이때 근의 공식은 -b±√(b²-4ac) / 2a로 정의된다. 이 식은 이차방정식의 해를 구하는 방식을 제시한 것이다.
2. 근의공식의 역사와 개발
근의공식은 알제브라 기원 전부터 계산 문제의 형태로 있었지만, 현대의 이차방정식을 정의하는 표현은 아라비아 수학자 무하마드 알 크와리즈미(우즈베키스탄 출신)가 10세기에 발표한 <알게브라>에서 분명해졌다.
근의공식은 오랜 세월 동안 발전해왔다. 실수계에서 근을 구하는 방식은 이단원(二段原)의 인도수학에서부터 있었다. 이외에도 중국, 인도, 중앙아시아 및 아랍 지역에서 전 세계적으로 발전되어왔다.
83년 경, 인도-아라비안 수학자 무함마드 알-카라지는 이차방정식 근의공식을 발전시키는 데 기여하였다. 이후 유럽들도 이 공식을 발전시키는 데 참여하였다. 가우스(1777~1855) 및 애드위드 케일리(1809~1891)가 이차방정식 근의공식에 대해 연구한 결과, 그 공식은 실수계와 복소수계에서 모두 성립하는 대표적인 공식이 되었다.
3. 근의공식의 수학적 전개
근의공식은 어느 정도 수학적인 전개를 거쳤다. 근의공식을 적용하기 위해서는 우선 이차방정식의 계수 a, b, c를 알아야 한다. 그런 다음 이차방정식에 근의공식을 대입하여 수식을 전개해야 한다.
예를 들어, x²+2x-3=0이라는 이차방정식이 있다. 이를 다음과 같이 전개할 수 있다.
– (x+1)² = 4
– x+1 = ±2
– 따라서 x = -3, 1
여기서 (x+1)² = 4라는 부분은 왼쪽 항을 완전제곱했다고 볼 수 있다.
4. 근의공식과 복소수
근의공식은 실수계와 복소수계에서 모두 성립한다. 그러나 일반적으로 이차방정식의 해 중에서 복소수 계에 속하는 해는 상상할 수 없는 것으로 여겨지는데, 이는 고등 수학을 다룰 때 처음 듣는 사실이다.
복소수 계에서의 근의공식은 실수 계에서의 근의공식과 구조적으로 동일하다. 다만, 복소수는 실수와 허수의 합으로 표현되어 있는데, 이를 이용해 수식을 전개하면 된다. 예를 들어, 방정식 x²+4x+5=0의 해는 x = -2±i가 된다.
5. 근의공식의 활용 예시
근의공식은 이차방정식의 해를 구하는 데 있어서 매우 중요한 역할을 한다. 이때 이차방정식은 물리학, 경제, 인구통계 등 다양한 분야에서 적용될 수 있기 때문에, 근의공식은 다양한 분야에서 활용된다.
가령, 어떤 기업이 매년 성장률을 계산해야 하는데, 이를 계산하기 위해서는 이차방정식을 이용할 수 있다. 또한, 인구통계학에서도 이차방정식을 이용하여 인구 조사 결과를 분석할 수 있다. 이런 식으로, 근의공식은 자연과학, 사회과학, 경제학에서 모두 활용될 수 있다.
6. 근의공식의 한계와 대안
근의공식은 이차방정식의 해를 구하는 데 매우 유용한 방법이지만, 한계도 존재한다. 첫째로, 선형방정식이나 이차 방정식의 해가 인위적으로 주어지는 경우에는 근의공식을 적용할 필요가 없다.
둘째로, 세 이상의 차수를 가진 방정식의 경우에는 근의 공식이 존재하지 않는다. 따라서 그 경우에는 다른 방법을 찾아야 한다.
셋째로, 근의공식을 이용하여 이차방정식의 근을 구하더라도, 그 해를 유추하는 과정에서 오차가 발생할 수 있다. 이는 수학문제에서 결국 결과가 적절한다고 받아들여지는 기준을 생각한다면, 근의공식이 불확실성을 감지하는데 그나마 도움을 주지만, 정교한 계산에는 한계가 있다는 것을 의미한다.
근의공식의 영어로는 Quadratic formula이다. 근의공식을 쓰는 이유는 이차방정식을 풀기 위해서이다. 근의공식을 만든 사람은 다양하지만, 대표적으로 알카리즈미, 가우스, 케일리 등이 있다. 짝수 근의공식은 이차방정식의 해 중에서 두 개가 항상 대칭이 되는 경우를 나타낸다.
근의공식은 복소수에 대해서도 적용 가능하며, 복소수로 표현된 해는 이차방정식에서 사용되는 방정식의 계수가 실수 계수일 때 구해진다.
근의공식에 대해 더 자세히 이해하고 싶다면, 근의공식 계산기나 이차방정식 증명에 대한 자료를 찾아보는 것이 좋다. 나무위키에도 근의공식에 대한 내용이 있으며, 자세한 내용을 참고할 수 있다.
FAQs
1. 근의공식은 어떤 수식을 표현하기 위한 것인가요?
근의공식은 이차방정식의 해를 구하기 위한 공식입니다. 이차방정식은 ax²+bx+c=0의 형태를 가지며, 이를 풀기 위해서는 근의공식이 필요합니다.
2. 근의공식을 쓰는 이유는 무엇인가요?
근의공식은 이차방정식의 해를 구하기 위한 가장 효과적인 방법 중 하나입니다. 이차방정식의 근을 구하는 방법 중 하나인 요동근법(메소드)보다 간단하고 정확하기 때문에 근의 공식이 많이 사용됩니다.
3. 근의공식을 만든 사람은 누구인가요?
근의공식은 오랜 세월 동안 계산 문제의 형태로 있었지만, 현대의 이차방정식을 정의하는 표현은 아라비아 수학자 무하마드 알 크와리즈미(우즈베키스탄 출신)가 10세기에 발표한 <알게브라>에서 분명해졌습니다. 이외에도 가우스와 케일리 등이 근의공식을 발전시켰습니다.
4. 짝수 근의공식이란 무엇인가요?
짝수 근의공식은 이차방정식의 해 중에서 두 개가 항상 대칭이 되는 경우를 나타냅니다. 이 경우 근의공식을 적용하여 해를 구하면 대칭인 두 개의 해를 얻을 수 있습니다.
5. 근의공식은 복소수에 대해서도 적용 가능한가요?
네, 근의공식은 복소수계에서도 모두 성립합니다. 다만, 이차방정식의 근을 구하는 경우, 실수 계와 복소수 계의 해가 있을 수 있고, 이에 따라 해를 유추할 수 있도록 분기를 나눠야 합니다.
6. 근의공식 계산기를 어디서 찾을 수 있나요?
인터넷에서 근의공식 계산기를 찾아 사용할 수 있습니다. 과학 계산기, 수학 계산기 등 다양한 정보 사이트에 접속하여 근의공식 계산기를 이용할 수 있습니다.
사용자가 검색한 키워드: 근의공식 뜻 근의 공식 영어로, 근의 공식 쓰는 이유, 근의 공식 만든 사람, 짝수 근의 공식, 근의 공식 허수, 근의 공식 나무위키, 근의 공식 계산기, 이차방정식 근의 공식 증명
Categories: Top 53 근의공식 뜻
[EBS 수학의 답] 이차방정식 – 13. 근의 공식의 유도 과정
여기에서 자세히 보기: b1.brokengroundgame.com
근의 공식 영어로
The quadratic formula is known for its versatility in providing solutions to the broadest range of quadratic equations. The formula states that the two roots of the equation, x1 and x2, are given by:
x1 = (-b + √(b^2 – 4ac))/(2a)
x2 = (-b – √(b^2 – 4ac))/(2a)
In the formula, the term under the square root sign, b^2 – 4ac, is called the discriminant. The discriminant is commonly used to determine the nature of the roots of a quadratic equation.
If the discriminant is positive, the quadratic equation has two real and distinct roots. If the discriminant is zero, the quadratic equation has one real and repeated root. If the discriminant is negative, the quadratic equation has two complex conjugate roots.
The origins of the quadratic formula can be traced back to ancient Babylonian and Indian civilizations who had an understanding of quadratic equations. Nevertheless, it was the ancient Greek mathematician Euclid who first derived the formula in his book Elements, written around 300 BCE. The formula was further refined by several other mathematicians, including al-Khwarizmi and Omar Khayyam in the Islamic Golden Age.
Today, the quadratic formula is an essential tool in various fields of science and engineering, including physics, chemistry, economics, and computer science.
Application of the Quadratic Formula
The quadratic formula can be used to solve any quadratic equation that is in the standard form of ax^2 + bx + c = 0. This equation represents a parabolic curve that intersects the x-axis at two points, where the roots are found.
When using the quadratic formula to solve a quadratic equation, all you need to do is to identify the values of a, b, and c in the equation and plug them into the formula. Once you have calculated x1 and x2, these values can be plotted on the coordinate plane to yield the parabolic curve.
Here is an example of how the quadratic formula can be used to solve a quadratic equation:
Solve for x: 6x^2 – 11x + 3 = 0
a = 6, b = -11, c = 3
x1 = (-(-11) + √((-11)^2 – 4*6*3))/(2*6) = 1/2 or 0.5
x2 = (-(-11) – √((-11)^2 – 4*6*3))/(2*6) = 3/2 or 1.5
Therefore, the roots of the quadratic equation 6x^2 – 11x + 3 = 0 are x1 = 0.5 and x2 = 1.5.
FAQs About the Quadratic Formula
1. What is the standard form of a quadratic equation?
The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants.
2. What is the discriminant?
The discriminant is the term under the square root sign in the quadratic formula, b^2 – 4ac. It is used to determine the nature of the roots of a quadratic equation.
3. What does it mean for the discriminant to be positive?
If the discriminant is positive, the quadratic equation has two real and distinct roots.
4. What does it mean for the discriminant to be zero?
If the discriminant is zero, the quadratic equation has one real and repeated root.
5. What does it mean for the discriminant to be negative?
If the discriminant is negative, the quadratic equation has two complex conjugate roots.
6. Can the quadratic formula be used to solve any quadratic equation?
Yes, the quadratic formula can be used to solve any quadratic equation that is in the standard form of ax^2 + bx + c = 0.
7. Who first derived the quadratic formula?
The ancient Greek mathematician Euclid first derived the quadratic formula in his book Elements, written around 300 BCE.
Conclusion
In summary, the quadratic formula is a powerful mathematical tool used to find the roots of quadratic equations in the standard form of ax^2 + bx + c = 0. This formula is versatile and can be used to solve a wide range of quadratic equations in various fields of science and engineering. Understanding the quadratic formula and its applications is essential for anyone seeking to excel in advanced mathematics.
근의 공식 쓰는 이유
근의 공식을 왜 쓰는가?
첫째로 근의 공식을 이해하고 활용하는 것은 방정식을 해결하는 데에 도움이 됩니다. 이차 방정식의 근은 전통적으로 근의 공식을 통해 구해왔으며, 이외에도 확률과 통계학, 물리학 등 다양한 학문에서 다양한 분야에서 응용됩니다.
둘째로, 근의 공식을 이해함으로써 무리한 단계를 줄일 수 있습니다. 예를 들어, 소인수분해, 부분 분수 등의 다른 수학적 단계를 사용하여 방정식을 해결할 수 있지만, 그보다 근의 공식을 사용하여 더 간단하고 빠른 방법이 있습니다.
셋째로, 근의 공식을 이해하고 활용함으로써 수학적 문제를 해결하는 데에 확신을 가질 수 있습니다. 수학적 문제 해결의 방법은 다양하지만, 문제 속에서 주어진 정보와 변수를 사용하여 문제를 해결하는 방법을 알고 있는 것은 매우 중요합니다.
FAQs
Q: 근의 공식 외에도 방정식의 근을 구하는 방법이 있을까요?
A: 네, 소인수분해, 부분 분수 등 다양한 수학적 단계를 사용하여 방정식의 근을 구하는 방법이 있습니다. 그러나 이러한 방법은 근의 공식보다 복잡하고 더 많은 단계를 요구합니다.
Q: 근의 공식을 외우지 않아도 방정식을 해결할 수 있나요?
A: 예, 근의 공식을 외우지 않아도 다른 수학적 단계를 사용하여 방정식의 근을 구할 수 있습니다. 그러나 근의 공식을 이해하고 활용할 수 있으면 방정식의 근을 더 빠르고 쉽게 구할 수 있습니다.
Q: 근의 공식을 이해하는 데에 얼마나 시간이 걸릴까요?
A: 그것은 개인적으로 달려있습니다. 일부 학생들은 근의 공식을 이해하는 데 시간이 걸리지 않을 수 있지만, 일부 학생들은 근의 공식을 이해하는 데 몇 번의 자습이 필요할 수 있습니다. 하지만, 근의 공식을 이해하는 데 시간을 투자하는 것은 충분히 가치있는 일입니다.
Q: 근의 공식을 외우는 방법은 무엇인가요?
A: 근의 공식을 외우는 방법은 다양하지만, 일반적으로 근의 공식을 직접 쓰는 것보다는 일련의 연습 문제를 통해 익숙해지는 것이 더 효과적입니다.
Q: 방정식의 근을 구하는 데에 근의 공식 외에 다른 중요한 수학 개념이 있나요?
A: 네, 상수항, 계수, 추가대, 진액, 완전제곱수 등 방정식을 이해하는 데 중요한 수학 개념이 많이 있습니다. 이러한 개념을 이해하고 활용하면 근의 공식을 사용하는 것보다 더 간편하고 효과적인 방법으로 방정식의 근을 구할 수 있습니다.
결론적으로, 근의 공식을 이해하고 활용하면 수학적 문제를 더 빠르고 쉽게 해결할 수 있습니다. 또한, 이러한 공식을 이해하고 활용함으로써 수학적 문제를 해결하는 데에 더 확신을 가질 수 있습니다. 매일 연습하고 익숙해지면, 근의 공식은 매우 유용한 수학 개념이 될 것입니다.
주제와 관련된 이미지 근의공식 뜻
![[EBS 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정 [EBS 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정](https://b1.brokengroundgame.com/wp-content/uploads/2023/06/hqdefault-2055.jpg)
근의공식 뜻 주제와 관련된 이미지 46개를 찾았습니다.


![이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기) 이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기)](https://blog.kakaocdn.net/dn/CFxKW/btqEljhxYt2/Kq0oLoyjzCIIYbRDFKkGYk/img.png)


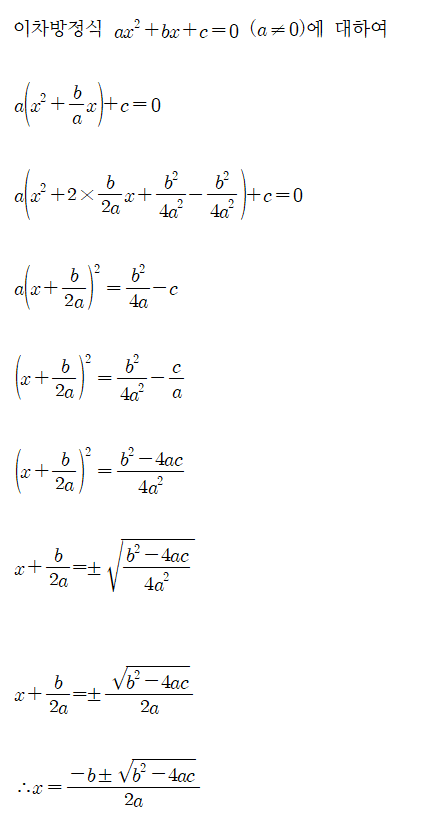
![중3수학] 이차방정식 단원 총정리 / 이차방정식의 뜻부터 근의 공식까지(#shorts 모음) - YouTube 중3수학] 이차방정식 단원 총정리 / 이차방정식의 뜻부터 근의 공식까지(#Shorts 모음) - Youtube](https://i.ytimg.com/vi/tiVMRhDTILE/maxresdefault.jpg)



![EBS 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정 - YouTube Ebs 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정 - Youtube](https://i.ytimg.com/vi/JmKNoFeZP4Y/maxresdefault.jpg)







![중3-1수학 [26강] 근의공식 유도과정 - YouTube 중3-1수학 [26강] 근의공식 유도과정 - Youtube](https://i.ytimg.com/vi/qSJqALuM6w4/maxresdefault.jpg)








![체크체크 베이직 수학 중 3-1 (2023년용) 도서 리뷰 : 수학의 기본을 쌓는 [체크체크베이직 중3-1] | YES24 블로그 - 내 삶의 쉼표 체크체크 베이직 수학 중 3-1 (2023년용) 도서 리뷰 : 수학의 기본을 쌓는 [체크체크베이직 중3-1] | Yes24 블로그 - 내 삶의 쉼표](https://image.yes24.com/mobileblogimage/blog/e/c/ecossuk/1637493016152.jpg)




![모듈식 수학 (상)] 2. 방정식과 부등식 (15) 이차방정식의 판별식 모듈식 수학 (상)] 2. 방정식과 부등식 (15) 이차방정식의 판별식](https://t1.daumcdn.net/cfile/tistory/9994C03F5BBC07120C)
Article link: 근의공식 뜻.
주제에 대해 자세히 알아보기 근의공식 뜻.
- 근 (수학) – 위키백과, 우리 모두의 백과사전
- 근의 공식, 근의 공식 유도, 짝수 공식 – 수학방
- 이차방정식의 근의 공식 이해하기 – 칸아카데미
- 근의 공식 – 이차방정식의 뜻과 풀이 (2) (개념+수학문제)
- [근의 공식] 이차방정식의 근의 공식 – Naver Blog
- 27. 이차방정식에서 근이란 무엇인가…?
- 근의 공식/quadratic formula – 수학사랑
더보기: b1.brokengroundgame.com/krblog

