근의공식 증명
근의공식은 대수학에서 중요한 개념이며, 많은 수학자들이 이를 연구했습니다. 이 공식은 일반적으로 미지수가 있는 다항식에서 근을 구하는 방법입니다. 근의공식은 수학을 이해하는데 중요한 역할을 합니다. 이 문서에서는 근의공식에 대한 정의와 근의공식의 증명에 대해 알아보겠습니다.
근의 공식이란 무엇인가?
근의공식은 다항식에서 루트의 근을 구하는 공식을 의미합니다. 예를 들어, 다음과 같은 다항식이 있을 때:
ax^2 + bx + c = 0
여기서 x는 미지수, 그리고 a, b, c는 상수입니다. 이 다항식이 0이 될 때, 이를 해결하기 위해 x의 값을 구해야 합니다. 이때, 근의공식을 사용하여 x를 찾을 수 있습니다.
제곱근의 개념과 성질
우선, 제곱근에 대한 개념을 이해해야 합니다. 제곱근은 양의 정수를 제곱한 결과로 얻어지는 값입니다. 예를 들어, 4의 제곱근은 √4 = 2입니다. 이때, √는 루트 기호를 의미합니다.
제곱근에는 몇 가지 성질이 있습니다. 양의 정수 a와 b에 대해 다음과 같은 성질이 성립합니다.
1. √(a x b) = √a x √b
2. √(a / b) = √a / √b
이러한 성질은 근의공식 증명에 매우 중요합니다.
근의공식의 증명에 대해서
근의공식은도스토예프스키(d’Alembert)와 라그랑주(Lagrange)에 의해 독립적으로 발견되었습니다. 근의공식의 제일 기본적인 증명은 베이지(Bézout)와 랑장(Lanz)에 의해 제공되었습니다.
근의공식의 증명은 다음과 같습니다.
우선, 2차 다항식 ax^2 + bx + c = 0에서 a ≠ 0일 경우를 생각해봅시다.
다음과 같은 공식을 이용하여 근의 공식을 증명합니다.
x = [-b ± √(b^2 – 4ac)] / 2a
우선, 이 공식이 어떻게 유도되었는지 알아보겠습니다. ax^2 + bx + c = 0을 정리하면 다음과 같이 됩니다.
x^2 + (b/a)x + (c/a) = 0
a ≠ 0 이므로, 양변에 a를 곱하면 다음과 같이 됩니다.
ax^2 + bx + c = 0
정리하면, 다음과 같은 공식이 유도됩니다.
x = [-b ± √(b^2 – 4ac)] / 2a
여기서, √(b^2 – 4ac)를 따로 분석해 보겠습니다. 우선, b^2 – 4ac가 음수인 경우에는 다음과 같은 형태로 변환할 수 있습니다.
√(b^2 – 4ac) = √-(b^2 – 4ac) = i√(4ac – b^2)
여기서 i는 허수입니다. 이 때, 앞서 소개한 제곱근의 성질을 이용하여 식을 정리할 수 있습니다. i^2 = -1 이므로, 다음과 같이 정리할 수 있습니다.
√(b^2 – 4ac) = i√(4ac – b^2) = √[(2a)x]^2 – (b^2 – 4ac)
따라서, 공식을 다음과 같이 정리할 수 있습니다.
x = [-b ± √(b^2 – 4ac)] / 2a
근의공식의 응용
근의공식은 선형 대수학, 미적분학, 수리 물리학 등의 영역에서 적용됩니다. 이를 통해 다양한 수학적 문제를 해결할 수 있습니다.
근의공식은 또한 공학 분야에서도 중요한 역할을 합니다. 예를 들어, 전기공학에서는 복소수 평면 위에서 삼각함수를 사용하는 것이 필요합니다. 이때, 근의공식을 사용하여 복소수의 표현을 단순화할 수 있습니다. 이는 회로 이론과 전기기술을 이해하는 데 큰 도움이 됩니다.
근의공식의 다양한 버전
근의공식은 다음과 같은 다양한 버전이 있습니다.
– 2차 근의공식: ax^2 + bx + c = 0
– 3차 근의공식: ax^3 + bx^2 + cx + d = 0
– 4차 근의공식: ax^4 + bx^3 + cx^2 + dx + e = 0
– 5차 근의공식: ax^5 + bx^4 + cx^3 + dx^2 + ex +f = 0
이러한 근의공식들은 각각의 차수에 맞게 유도됩니다.
근의공식의 역사와 개발 과정
근의공식은 16세기 이탈리아 수학자 타르탈리아(Cardano)와 후계자들에 의해 발견되었습니다. 이후 17세기 프랑스 수학자 페르마(Fermat)에 의해 3차 방정식의 근의 공식이 발견되었습니다. 이후 18세기 프랑스 수학자 라그랑주(Lagrange)와 페럴(Ferrari)에 의해 4차 방정식의 근의 공식이 발견되었습니다.
근의공식은 수학을 이해하는데 매우 중요한 개념이며, 다양한 분야에서 적용됩니다. 현재는 근의공식을 포함한 다양한 수학적 개념이 컴퓨터 프로그래밍에도 적용되고 있습니다.
FAQs
Q. 근의 공식을 쓰는 이유는 무엇인가요?
A. 근의 공식은 다항식에서 근을 찾는 방법을 제공합니다. 이를 통해 수학적 문제를 쉽게 해결할 수 있습니다.
Q. 근의 공식을 만든 사람은 누구인가요?
A. 근의공식은 다양한 수학자들에 의해 발견되었습니다. 이탈리아 수학자 타르탈리아(Cardano), 프랑스 수학자 페르마(Fermat), 라그랑주(Lagrange), 페럴(Ferrari) 등이 그 중 일부입니다.
Q. 근의 공식은 어떻게 활용될 수 있나요?
A. 근의공식은 대수학뿐만 아니라 선형 대수학, 미적분학, 수리 물리학 등의 영역에서 적용됩니다. 또한, 공학 분야에서도 중요한 역할을 합니다.
Q. 근의 공식에 대한 계산기는 어디에서 찾을 수 있나요?
A. 근의 공식에 대한 계산기는 인터넷에서 다양한 사이트에서 찾을 수 있습니다.
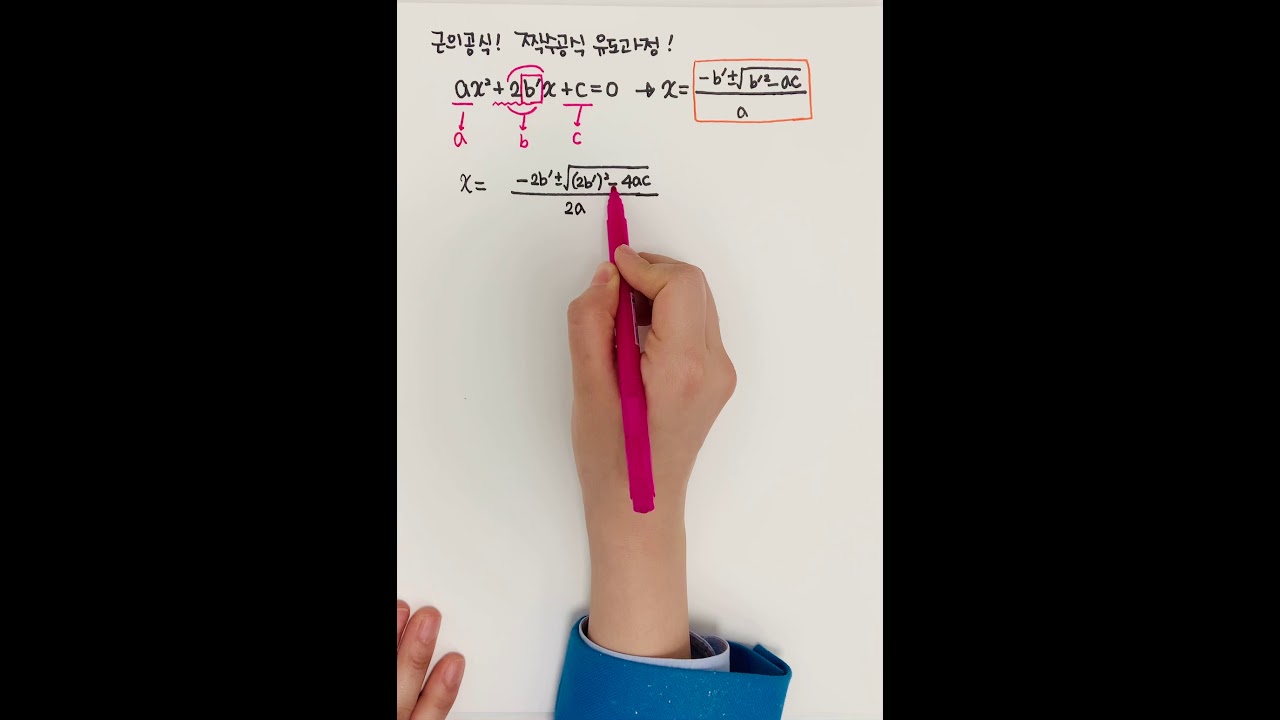
Q. 짝수 근의 공식은 무엇인가요?
A. 짝수 근의 공식은 일반적인 근의 공식보다 쉽게 유도됩니다.
Q. 근의공식 학년은 어디에서 배울 수 있나요?
A. 근의공식은 중·고등학교 수학에서 다루는 내용입니다.
Q. 4차 방정식 근의 공식은 어떻게 유도되나요?
A. 4차 방정식 근의 공식은 라그랑주(Lagrange)와 페럴(Ferrari)에 의해 발견되었습니다.
Q. 근의 공식 정의는 무엇인가요?
A. 근의공식은 다항식에서 루트의 근을 구하는 공식을 의미합니다.
사용자가 검색한 키워드: 근의공식 증명 근의 공식 쓰는 이유, 근의 공식 만든 사람, 근의 공식 활용, 근의 공식 계산기, 짝수 근의 공식, 근의공식 학년, 4차 방정식 근의 공식, 근의 공식 정의
Categories: Top 33 근의공식 증명
조조쌤 중3 수학 근의공식 증명! 근의공식 원리에 대해서 배워봅시다!
여기에서 자세히 보기: b1.brokengroundgame.com
근의 공식 쓰는 이유
근의 공식이란?
근의 공식은 일반적인 이차방정식의 근을 구하는 방법입니다. 이차방정식은 다음과 같은 형태를 가집니다. ax² + bx + c = 0 (a ≠ 0)
여기서 a,b,c는 실수이고, x는 변수입니다. 이차방정식의 근을 구하는 것은 이 방정식이 만족하는 x의 값을 찾는 것입니다. 근의 공식은 이 값을 쉽게 계산할 수 있도록 만들어진 공식입니다.
근의 공식의 수식은 다음과 같습니다.
x = (-b ± √(b² – 4ac))/2a
여기서 √는 제곱근을 의미합니다. 이 식을 이용하여 이차방정식의 근을 구할 수 있습니다.
근의 공식을 쓰는 이유는 무엇인가요?
근의 공식은 이차방정식의 근을 구하는 가장 쉬운 방법 중 하나입니다. 이차방정식은 다양한 분야에서 자주 사용되며, 이에 따라 근의 공식 또한 매우 중요합니다.
가령, 금융 분야에서는 이차방정식을 이용하여 이자율, 현금흐름 등을 계산합니다. 또한 물리학에서도 이차방정식이 자주 사용됩니다. 예를 들어, 허블 우주망원경을 이용하여 이차방정식을 이용해 우주의 시간과 거리를 계산할 수 있습니다.
무엇보다도, 근의 공식은 수학적인 지식을 활용하여 복잡한 문제를 해결하는 것에 매우 유용합니다. 근의 공식을 이용하면 다양한 이차방정식을 효율적으로 풀 수 있습니다. 이로 인해, 수학적인 문제를 해결하는 데에 근의 공식은 핵심적인 역할을 합니다.
근의 공식의 유용성은 무엇인가요?
근의 공식은 어떠한 이차방정식도 풀 수 있다는 점에서 유용합니다. 이때 이차방정식이 복소수 근을 가질 경우에도 근의 공식을 이용하여 쉽게 푸는 것이 가능합니다. 또한, 근의 공식은 다른 수학적인 개념과 함께 병행하여 이용할 수 있습니다.
가령, 근의 공식은 이차함수와 관련이 있습니다. 이차함수는 실수 전체에 대해 정의되는 함수입니다. 이러한 함수의 극점과 최솟값, 최댓값을 구할 때에도 근의 공식을 이용하여 쉽게 접근할 수 있습니다.
여러분이 어떤 형태의 이차방정식을 푸는 데 어려움을 겪었을 때, 근의 공식은 유용합니다. 이를 통해, 어려운 수학 문제를 해결할 수 있습니다.
근의 공식을 이용할 때 주의해야 할 점이 있나요?
근의 공식을 이용할 때에는, 우선 이차방정식의 계수인 a, b, c가 실수이어야 합니다. 만약 이들 계수 중에 하나가 복소수일 경우에는, 다른 방식을 이용하여 이차방정식을 풀어야 합니다.
또한, 이 식을 이용하는 경우 제곱근의 계산이 필요합니다. 제곱근의 값은 긴 계산 과정을 거쳐 구할 수 있습니다. 대신, 소수 나누기와 제곱근을 이용하는 방법, 혹은 그래프로 나타내어 근을 구하는 방법이 있습니다.
마지막으로, 근의 공식은 허수방정식에서도 사용할 수 있습니다. 그러나 허수방정식의 경우에는 복소수에 대한 지식이 필요합니다. 따라서, 본질적으로 복소수에 대한 지식을 갖고 있어야 이를 알맞게 사용할 수 있습니다.
FAQs:
1. 근의 공식은 어떻게 유도될까요?
근의 공식은 이차방정식 ax² + bx + c = 0(a ≠ 0)에서 시작합니다. 우리는 다음과 같은 식으로 시작합니다. ax² + bx + c = a(x-h)² + k
여기서, x = h + t 라고 가정합니다. 그러면, 이 식은 다음과 같이 변형됩니다. ax² + bx + c = a(h² + 2ht + t²) + b(h + t) + c
이를 정리하면, at² + (2ah + b)t + (ah² + bh + c – ak) = 0입니다.
우리는 t를 구하기 위해 이 식의 해를 구해야 합니다. 이는 다음과 같은 이차방정식의 형태를 가지므로, 근의 공식을 이용하여 해를 구할 수 있습니다.
at² + (2ah + b)t + (ah² + bh + c – ak) = 0
이를 통해, x = h + t 형태로 x의 값을 구할 수 있습니다.
2. 어디에서 근의 공식을 사용할까요?
근의 공식은 이차방정식과 함께 사용되며, 이차방정식은 다양한 분야에서 사용됩니다. 예를 들어, 금융 분야에서는 이차방정식을 이용하여 이자율, 현금흐름 등을 계산합니다. 또한 물리학에서도 이차방정식이 자주 사용됩니다. 예를 들어, 허블 우주망원경을 이용하여 이차방정식을 이용해 우주의 시간과 거리를 계산할 수 있습니다.
3. 근의 공식은 복소수 근도 구할 수 있나요?
네, 근의 공식은 여러 유형의 이차방정식에 대해 적용할 수 있으며, 복소수 근을 구할 수 있습니다.
4. 근의 공식을 사용할 때 주의할 점이 있나요?
근의 공식을 사용할 때에는, 우선 이차방정식의 계수인 a, b, c가 실수이어야 합니다. 만약 이 중 하나라도 복소수일 경우, 다른 방식을 이용하여 이차방정식을 풀어야 합니다. 또한, 이용하는 방법에 따라 제곱근의 계산이 필요합니다. 제곱근의 값은 복잡한 계산을 거쳐 구할 수 있으며, 다른 방법을 이용하여 계산할 수도 있습니다. 따라서 이를 푸는 데에는 계산 능력이 필요합니다.
근의 공식 만든 사람
Abu al-Hasan al-Uqlidisi – Early Life
Abu al-Hasan al-Uqlidisi was born in Uqlid, a city located in present-day Iraq, in 952 A.D. He was a Muslim scholar and mathematician who is known for his work in algebra and arithmetic. Abu al-Hasan al-Uqlidisi grew up in the Islamic Golden Age, a period of intellectual and cultural growth in the Islamic world. This period saw the flourishing of the sciences, arts, and mathematics in the Islamic world.
Abu al-Hasan al-Uqlidisi – Contributions
Abu al-Hasan al-Uqlidisi is known for his contribution to the field of mathematics, particularly in the area of algebra. He is the author of Kitāb al-fuṣūl fī al-ḥisāb al-Hindī (The Book of Chapters on Indian Arithmetic) and Al-jāmʿ wal-tafrīq bi-ḥisāb al-ḥind (Addition and Subtraction in Indian Arithmetic). Abu al-Hasan al-Uqlidisi is also credited with the development of the method of finding roots of quadratic equations. This method is known as ‘The person who created the formula for the roots’ or ‘The quadratic formula’.
The quadratic formula is used to find the roots of a quadratic equation. A quadratic equation is an equation in which the highest power of the variable is two. The quadratic formula is given as follows:
x = (-b ± √b² – 4ac) / 2a
Where ‘a’ , ‘b’ and ‘c’ are constants.
The quadratic formula is used extensively in the field of mathematics, science, engineering, and technology. It is a fundamental tool for solving various mathematical problems involving quadratic equations.
Abu al-Hasan al-Uqlidisi’s contributions to the field of mathematics did not end with the quadratic formula. He is also known for his work in the area of arithmetic, particularly in the use of decimal fractions. He introduced the Hindu-Arabic number system to the Islamic world and wrote extensively on the use of decimal fractions. His work on decimal fractions was later translated into Latin and adopted by the European mathematicians.
FAQs
Q1. What is the quadratic formula?
A. The quadratic formula is used to find the roots of a quadratic equation. A quadratic equation is an equation in which the highest power of the variable is two. The quadratic formula is given as follows:
x = (-b ± √b² – 4ac) / 2a
Where ‘a’ , ‘b’ and ‘c’ are constants.
Q2. Who introduced the quadratic formula?
A. Abu al-Hasan al-Uqlidisi, also known as ‘The person who created the formula for the roots’ is credited with the development of the method of finding roots of quadratic equations. This method is known as ‘The quadratic formula’.
Q3. What are the applications of the quadratic formula?
A. The quadratic formula is used extensively in the field of mathematics, science, engineering, and technology. It is a fundamental tool for solving various mathematical problems involving quadratic equations.
Q4. What are decimal fractions?
A. A decimal fraction is a fraction whose denominator is a power of ten. The decimal point is used to separate the numerator and the denominator. Decimal fractions are used extensively in the arithmetic of numbers.
Q5. Who introduced decimal fractions?
A. Abu al-Hasan al-Uqlidisi is known for his work in the area of arithmetic, particularly in the use of decimal fractions. He introduced the Hindu-Arabic number system to the Islamic world and wrote extensively on the use of decimal fractions.
Abu al-Hasan al-Uqlidisi – Legacy
Abu al-Hasan al-Uqlidisi’s contributions to the field of mathematics have had a considerable impact on the development of mathematics. His introduction of the Hindu-Arabic number system to the Islamic world revolutionized the field of arithmetic. His work in the area of algebra, particularly in the development of the quadratic formula, has been a fundamental tool for solving various mathematical problems.
Abu al-Hasan al-Uqlidisi’s work has been recognized and celebrated throughout history. The asteroid ‘Uqlidisi’ has been named after him to honor his contribution to the field of mathematics. His work on decimal fractions has been translated into Latin and adopted by the European mathematicians. His contribution to the field of mathematics continues to inspire and influence mathematicians around the world.
Conclusion
Abu al-Hasan al-Uqlidisi, the person who created the formula for the roots, is a renowned mathematician who lived in the 10th century. He is known for his work in the area of algebra, particularly in the development of the quadratic formula. His contribution to the field of mathematics has been fundamental in solving various mathematical problems. His work on decimal fractions has been adopted by the European mathematicians and has had a considerable impact on the development of arithmetic. Abu al-Hasan al-Uqlidisi’s contributions continue to inspire and influence mathematicians around the world.
근의 공식 활용
근의 공식 활용 in Korean
Quadratic equations are used extensively in mathematics, science, engineering, and many other fields. The 근의 공식 can help us find solutions to these equations easily and quickly. The formula itself is quite simple and is widely used in mathematics textbooks, exams, and problems. It is derived from the quadratic equation using the complete the square method.
The quadratic formula can be written as:
X = (-b ± sqrt(b^2-4ac))/(2a)
where X is the solution(s) of the quadratic equation, a, b, and c are constants, and sqrt represents the square root of the expression.
For example, consider the equation x2 + 4x – 5 = 0. We can find the solution(s) of this equation using the quadratic formula as follows:
a = 1, b = 4, c = -5
X = (-4 ± sqrt(16+20))/(2*1)
X = (-4 ± sqrt(36))/2
X1 = (-4 + 6)/2 = 1
X2 = (-4 – 6)/2 = -5
The solutions of the equation are x = 1 and x = -5.
Let’s look at some examples of how the 근의 공식 can be used in Korean:
Example 1:
한 친구가 자신의 정원에 16m^2의 면적을 가진 정사각형을 만들고자 합니다. 하지만 이를 만드는데 쓸 수 있는 벽돌의 면적은 각각 2m^2과 1m^2입니다. 이 친구가 몇 개의 벽돌을 사용해야 할까요?
Translation: A friend wants to make a square garden with an area of 16m^2 in his front yard. However, he only has bricks with an area of 2m^2 and 1m^2. How many bricks does he need to use?
Solution: Let’s assume the side of the square is x. Then, the area of the square is x^2. We can write the equation as x^2 = 16. Rearranging this equation, we get x^2 – 16 = 0. Applying the quadratic formula, we get:
a = 1, b = 0, c = -16
X = (0 ± sqrt(0+64))/(2*1)
X1 = 4, X2 = -4
Since x cannot be negative, the only valid solution is x=4. This means that the square has a side length of 4m. Therefore, the number of 2m^2 bricks needed is (4/2)^2=4 and the number of 1m^2 bricks needed is (4*4)-(4*2)=8. So, the friend needs 4 2m^2 bricks and 8 1m^2 bricks.
Example 2:
어느 자전거 길 경기에서 A, B 두 선수가 있는데, A 선수가 B 선수보다 2h^-1가 빠릅니다. 경기가 끝나고 나서 구조대원들이 B 선수가 산소 차단 현상으로 힘들어 하는 것을 알게 됩니다. 그럼 A 선수는 멈춰야 할까요? 그렇다면, 몇 시간 후에 멈추어야 할까요? 둘 다 100km를 달리고 있다고 가정합니다.
Translation: In a bicycle race, there are two players A and B. A is 2h^-1 faster than B. After the race, rescue workers realize that B is struggling due to oxygen deprivation. Should A stop? If so, after how many hours should he stop? Assume that both players are cycling for 100km.
Solution: Let the speed of B be x km/h. Then, the speed of A is (x+2) km/h. The time required for both players to cycle 100km is given by:
100/x + 100/(x+2)
Simplifying this expression, we get:
200x + 200 = x^2 + 2x^2 + 4x
3x^2 + 4x – 200 = 0
Using the quadratic formula, we get:
a = 3, b = 4, c = -200
X = (-4 ± sqrt(16+2400))/(2*3)
X1 = 10, X2 = -20/3
Since the time cannot be negative, the valid solution is X1 = 10. Therefore, both players would cycle for 10 hours before A stops.
FAQs:
Q. What is the difference between a linear and quadratic equation?
A. A linear equation is an equation of the form ax+b = 0, where a and b are constants and x is the variable. The solution of a linear equation is always a single value that satisfies the equation. On the other hand, a quadratic equation is an equation of the form ax2 + bx + c = 0, where a, b, and c are constants, and x is the variable. The solution of a quadratic equation is one or two values that satisfy the equation.
Q. Can the quadratic formula be used to solve equations with variable exponents?
A. No, the quadratic formula cannot be used to solve equations with variable exponents. The formula only applies to quadratic equations of the form ax2 + bx + c = 0.
Q. Can the quadratic formula be used to solve complex numbers?
A. Yes, the quadratic formula can be used to solve complex numbers. In this case, the values of a, b, and c may be complex numbers, and the solutions will also be complex numbers.
Q. What is the significance of the discriminant in the quadratic formula?
A. The discriminant, which is the expression under the square root in the quadratic formula, provides information about the nature of the solutions of the quadratic equation. If the discriminant is positive, the equation has two real solutions. If the discriminant is zero, the equation has one real solution. If the discriminant is negative, the equation has two complex solutions.
Conclusion
The utilization of the quadratic formula, or 근의 공식 활용, is an important skill in mathematics that can help us solve various problems. The formula itself is quite simple and requires only basic algebraic manipulation. By applying this formula to real-world situations, we can gain a deeper understanding of how to use mathematics to solve practical problems. Whether you are a student, a scientist, or an engineer, the quadratic formula will undoubtedly be a useful tool in your mathematical toolkit.
주제와 관련된 이미지 근의공식 증명

근의공식 증명 주제와 관련된 이미지 22개를 찾았습니다.
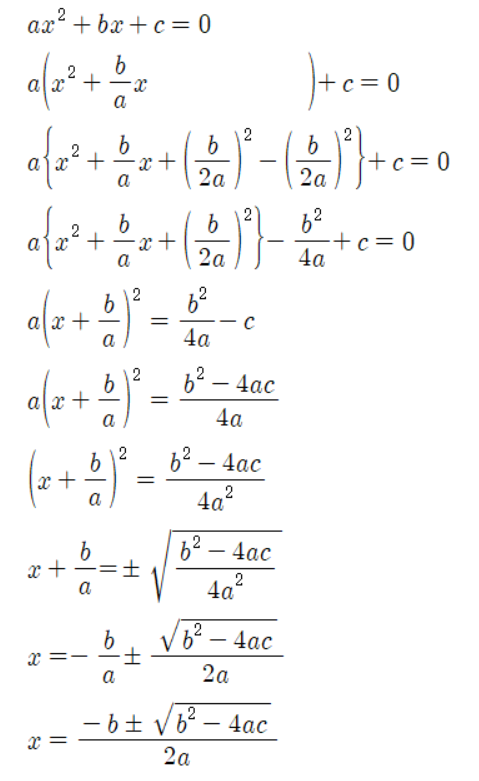

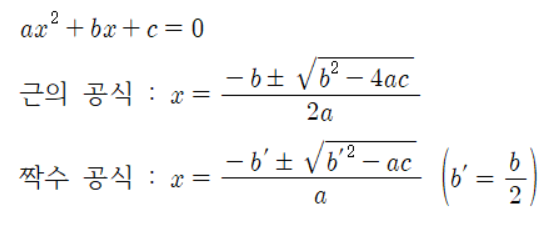


![이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기) 이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기)](https://blog.kakaocdn.net/dn/b16TIv/btqEljBSogl/AskNAzMjpxr8NvnoGImOlK/img.png)




![근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그 근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAxNzA3MThfMjgy/MDAxNTAwMzAzNjcwODM5.0Ko4eayHLraJjbWm_hrgK5JkmFTP7Ua85L_GU76sRncg.91v_26VXmz4pH4niVQckwPahti1BvTE2oqfwWng6pcIg.JPEG.pss2072/%EA%B7%BC%EC%9D%98%EA%B3%B5%EC%8B%9D_%EC%9C%A0%EB%8F%84.jpg?type=w420)
![중학 기본개념] 근의 공식, 짝수 근의 공식 중학 기본개념] 근의 공식, 짝수 근의 공식](https://t1.daumcdn.net/cfile/tistory/210B884055C0B6C21F)





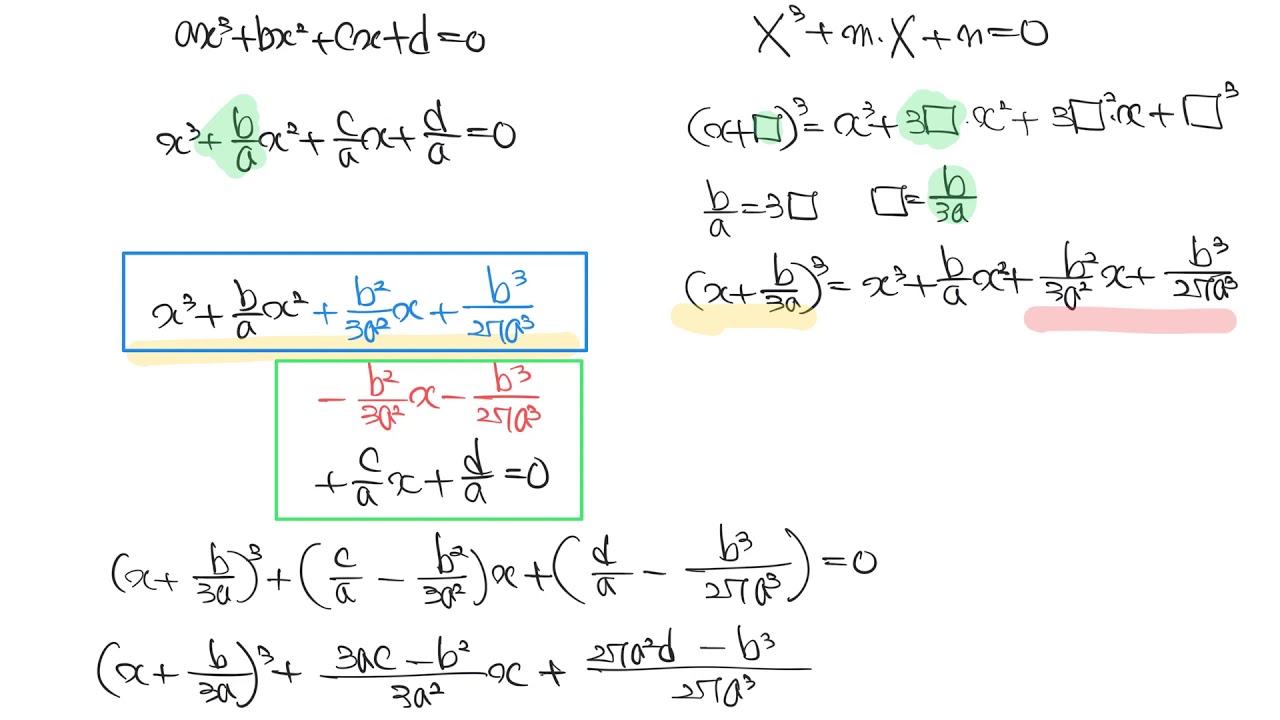








![모듈식 수학 (상)] 2. 방정식과 부등식 (13) 이차방정식의 풀이(근의공식) 모듈식 수학 (상)] 2. 방정식과 부등식 (13) 이차방정식의 풀이(근의공식)](https://t1.daumcdn.net/cfile/tistory/99E07E365BBC06C607)



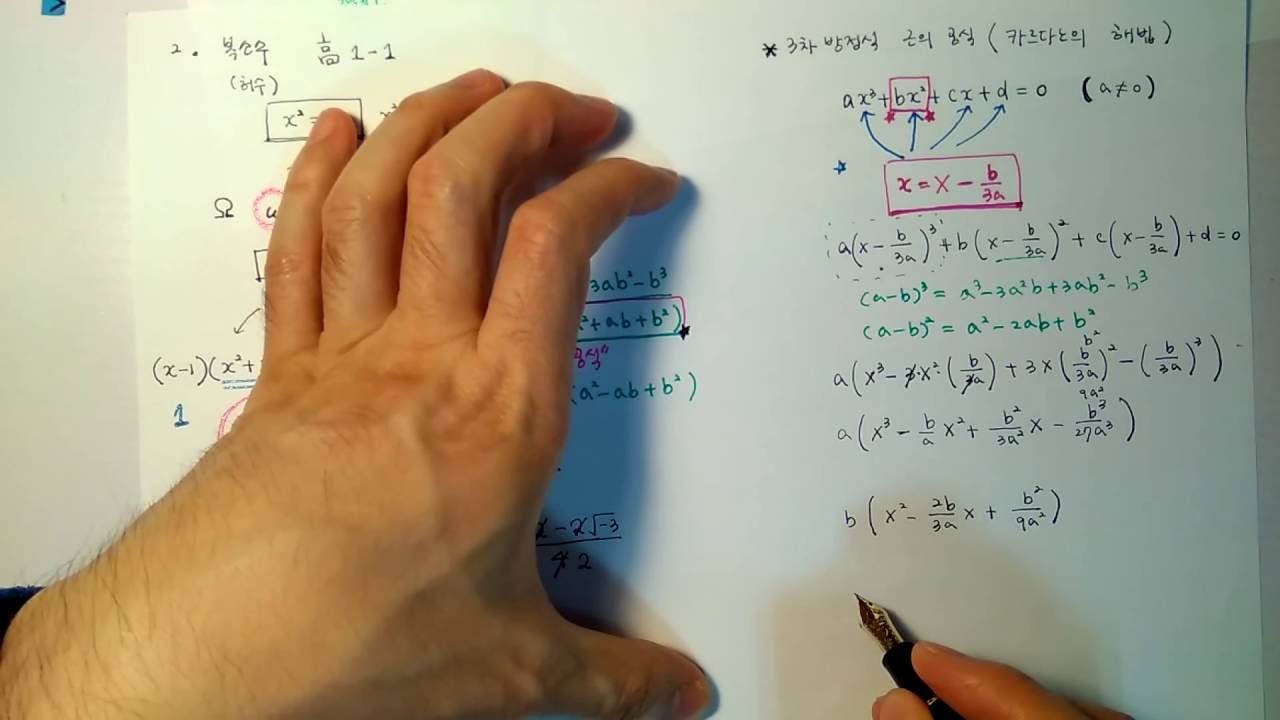
![중학 기본개념] 근의 공식, 짝수 근의 공식 중학 기본개념] 근의 공식, 짝수 근의 공식](https://t1.daumcdn.net/cfile/tistory/2347504655C0B6AE24)









![근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그 근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/20160608_290/pss2072_1465313050557Hn1F1_JPEG/%B1%D9%C0%C7%B0%F8%BD%C4.jpg?type=w420)
Article link: 근의공식 증명.
주제에 대해 자세히 알아보기 근의공식 증명.
- 근의 공식, 근의 공식 유도, 짝수 공식 – 수학방
- 근의 공식 증명 복습 – 칸아카데미
- [이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 …
- 근의 공식과 증명 – Playdaddy – 티스토리
- 짝수 근의 공식 (이차방정식 짝수 공식) – 모든 수학
- [이차방정식]근의 공식 및 유도하기 – 제이의 집
더보기: b1.brokengroundgame.com/krblog

