극한 공식
1. 극한 공식 개념 소개
A limit is a fundamental concept in mathematics that indicates how a function behaves when its input is close to a particular value or as the input approaches infinity. The limit is the value that the function appears to be approaching, even though it may not be there at the exact point. A formal definition of a limit is that it is a way to describe the behavior of a function as the input approaches a specific value.
In simpler terms, a limit considers the behavior of a function when its x-value approaches a particular value, say x=a. The limit tends to give the value or direction of the function around the point where x=a. In other words, the limit indicates where the function appears to be heading as it approaches x=a.
A limit can be evaluated using several methods, including direct substitution, factoring, multiplying by a conjugate, and using the squeeze theorem. To evaluate limits, students must understand the algebraic properties of limits and how to find undefined limits. The basic rules of limits include the sum and product rules, power rule, quotient rule, and algebraic rule.
2. 극한 공식의 적용 방법 및 종류
The application of limits is essential in various functions such as derivatives, integrals, and differential equations. Limits play an essential role in describing the behavior of functions at holes, jumps, and other discontinuities. The various types of limits include one-sided limits, infinite limits, and limits at infinity.
One-Sided Limits
A one-sided limit is a limit that exists only when the function approaches the value from one direction. In other words, it determines the behavior of the function as the input approaches the particular value from one side. One-sided limits are represented by symbols + or -. For example:
lim x→2^+ f(x) represents the limit of f(x) as x approaches 2 from the right (greater than 2)
lim x→2^- f(x) represents the limit of f(x) as x approaches 2 from the left (less than 2)
Infinite Limits
Infinite limits occur when the function reaches a value of positive or negative infinite as the input approaches a particular value. Infinite limits are represented by the symbols ∞ or – ∞. For example:
lim x→-4 f(x) = +∞ represents that the value of f(x) approaches infinity as x approaches -4.
Limits at Infinity
Limits at infinity are limits in which the function approaches an infinite value as the input grows exponentially. The limits at infinity are represented as lim x→±∞. For example:
lim x→∞ f(x) represents the limit of f(x) as x approaches infinity.
lim x→-∞ f(x) represents the limit of f(x) as x approaches negative infinity.
3. 극한 공식 계산법 및 예제
The calculation of limits involves finding the value of the function at every point where the input variable approaches a particular value. The calculation of limits can be done in various ways, including substitution, factoring, and algebraic manipulation. Let us consider some examples to illustrate how limits can be calculated.
Example 1:
Evaluate the limit of the function f(x) = (2x+5)/ (x-1) as x approaches 1.
We substitute the value of 1 for x in the expression (2x+5)/(x-1) to find that 2/0 is undefined. In this case, when we substitute x=1, we get 0 in the denominator, and division by 0 is undefined. However, from the algebraic manipulation below, we can see that the numerator approaches 9 as x approaches 1.
(2x+5)/(x-1) = [2(x-1)+9/(x-1)]
lim x→1 (2x+5)/(x-1) = lim x→1 [2(x-1)+9/(x-1)] = 9.
Therefore, the limit of the function f(x) as x approaches 1 is 9.
Example 2:
Evaluate the limit of the function f(x) = x^3-10x^2+3x+5 as x approaches -2.
We substitute -2 for x to get f(-2) = 20. However, this is not the limit that we are seeking. We can factor the expression f(x) as shown below:
(x^2-7x-5)(x+2)
Thus, we can see that (x^3-10x^2+3x+5) can be factored as (x+2)(x^2-7x-5). By simplifying and factoring further, we can express the limit as follows:
lim x→-2 f(x) = lim x→-2 [(x+2)(x^2-7x-5)/(x+2)] = lim x→-2 (x^2-7x-5) = -21
Hence, the limit of the function f(x) as x approaches -2 is -21.
4. 극한 공식의 활용론: 미분 및 적분
Limits are essential concepts in calculus and have many practical applications in several fields. The derivative of a function is a calculus concept that is defined as the rate of change of a function at a particular point. The derivative of a function f(x) is expressed mathematically as:
d/dx f(x) = lim Δx → 0 (f(x+ Δx) – f(x))/ Δx
where Δx is the change in input value as it approaches a particular value of x. The derivative is an application of limits and measures how much the function changes concerning the input changes.
The integral of a function is the inverse concept of the derivative. An integral measures the area under the curve of a function in a given range of values. In calculus, an integral is defined as:
f(x) dx = lim Δx → 0 ∑f(x)Δx
The integral of a function helps to solve real-world problems such as calculating the area under a curve, calculating the velocity during motion, and the energy demanded in the use of electricity.
5. 극한 공식의 역사와 의의
Limits were first introduced in Greek mathematics and were later developed by mathematicians in the 17th century. John Wallis, a British mathematician, first introduced the term limit in his book Introduction to Algebra. The development of limits led to the discovery of calculus by Isaac Newton and Gottfried Leibniz.
Limits are essential in calculus and are used to calculate derivatives, integrals, and other important mathematical concepts. Limits are useful in describing the behavior of functions at points of discontinuity and in solving real-world problems. Without limits, calculus and other areas of mathematics would not exist.
6. 극한 공식의 한계점 및 대안 방안
While limits are useful in describing the behavior of functions, they have some limitations. One significant limitation of limits is that they can be difficult to calculate, especially when dealing with complex functions or equations. Another challenge is that some functions do not have limits, or they may have different limits from both sides, leading to indeterminate forms. In such cases, other techniques like L’Hopital’s rule, using the squeeze theorem or Taylor series expansion can be used.
Other alternative methods include using a graphing calculator that can handle limits or using a limit calculator. Limit calculators can be found online and generate instant solutions to various limits.
In conclusion, 극한 공식 is a crucial concept in mathematics and plays a significant role in calculus and other fields of science and engineering. The article explained the concept of limits, their application, calculation, and their use in derivatives and integrals. Despite its limitations, limits have a profound impact on mathematical computation and herald a new dawn of discoveries in mathematical theories and applications.
사용자가 검색한 키워드: 극한 공식 극한 계산기, 극한법칙 증명, 극한 성질, 함수의 극한 수학자, 초월함수의 극한, 로그함수 극한 증명, 극한 기호, 자연로그 극한
Categories: Top 99 극한 공식
27. 함수의 극한 – 개념정리1
여기에서 자세히 보기: b1.brokengroundgame.com
극한 계산기
극한 계산기란 무엇인가?
극한 계산기는 수학적으로 복잡한 계산을 매우 빠르게 수행하는 기계입니다. 이 기계는 정확한 계산 뿐만 아니라, 미분, 적분, 행렬 연산과 같은 다양한 수학적 계산을 수행할 수 있습니다. 또한, 극한 계산기는 수치해석 및 과학 기술 계산에 널리 사용됩니다.
극한 계산기가 작동하는 방식은 무엇인가?
극한 계산기는 CPU와 RAM, 소프트웨어 등의 하드웨어와 소프트웨어로 이루어져 있습니다. CPU는 중앙 처리 장치로써 계산기능을 수행하며, RAM은 데이터를 저장하는 기능을 수행합니다. 극한 계산기에는 편리한 사용을 위한 여러가지 기능들이 탑재되어 있습니다. 예를 들면, 2D 및 3D 그래프 생성, 각종 유닛 변환, 유용한 math solver 등의 기능이 있습니다.
이 기계는 고속으로 연산을 수행할 수 있으며, 우리가 잘 알고 있는 정보 기술산업의 발전으로 여기에 사용되는 알고리즘과 데이터베이스 및 효율적인 하드웨어가 탑재되어 성능이 향상되었습니다.
극한 계산기의 중요성은 무엇인가?
극한 계산기는 매우 복잡한 수학적 계산을 처리하는 더 나은 방법을 제공합니다. 수학적인 문제를 해결하고 데이터에서 핵심 정보를 끌어내기 위해서는 극한 계산기가 매우 중요합니다. 실제로 이 기술은 저명한 수학자들도 사용하는 기술입니다.
또한 극한 계산기는 여러 필드에서 사용됩니다. 예를 들면, 공학, 경제학, 통계학, 물리학, 화학 등과 같은 분야에서 수학적인 문제 해결 및 데이터 분석에 사용됩니다. 엔지니어링 산업, 의료 분야, 금융 기관 등 여러 산업 및 부문에서는 극한 계산기 없이는 일할 수 없을 정도로 중요합니다.
극한 계산기를 사용하는 이유는 무엇인가?
극한 계산기는 수학적으로 복잡한 계산을 더 빠르고 정확하게 수행할 수 있습니다. 또한 이 기술은 인간의 실수 가능성을 다소 낮출 수 있습니다. 때문에 수학적인 문제를 해결하기 위해 시간과 노력을 절감할 수 있습니다.
또한 극한 계산기는 대부분의 경우 고급 수치 계산에 대해 다른 계산기보다 뛰어나며, 이를 통해 수치 해석, 과학기술 연구, 인공지능 및 기계 학습 분야 등에서 얻을 수 있는 결과에 대한 정확성 및 효율성을 향상시킵니다.
FAQs:
1. 극한 계산기를 어디에서 사용할 수 있는가?
극한 계산기는 수학 필드의 다른 분야에서 필요로 하는 많은 계산에 사용됩니다. 예를 들면, 미분, 적분, 행렬 연산과 같은 수학 계산, 공학 분야에서의 문제 해결, 의료 분야에서의 확률 계산 등에서 사용할 수 있습니다.
2. 극한 계산기는 어느 정도의 정확성을 보장할 수 있는가?
극한 계산기의 정확성은 소프트웨어 및 하드웨어의 품질에 따라 달라집니다. 일반적으로, 이 기술은 매우 높은 정확성을 보장합니다. 그러나 사용자가 입력한 데이터에 대한 오류가 있는 경우에는 정확도가 낮아질 수 있습니다.
3. 극한 계산기는 어떤 종류가 있는가?
극한 계산기에는 다양한 종류가 있습니다. 일반적으로, 소프트웨어 기반 극한 계산기, 하드웨어 기반 극한 계산기, 그리고 이 둘을 결합한 극한 계산기 등이 있습니다. 이러한 극한 계산기는 거의 모든 분야에서 사용되며, 기능적으로 서로 다릅니다.
4. 극한 계산기를 사용하기 위해서는 어떤 기술 및 지식이 필요한가?
극한 계산기를 사용하기 위해서는 일반적으로 수학 지식과 계산 능력이 필요합니다. 이는 극한 계산기를 사용하는 목적에 따라 다릅니다. 일부 목적에서는 수학과 과학을 전문적으로 연구하는 학자들 뿐 아니라 프로그래밍과 컴퓨터 공학 기술에도 능숙해야 합니다.
5. 다른 계산기와 극한 계산기의 차이점은 무엇인가?
일반적인 계산기는 소형 계산 전자 기기입니다. 이 계산기는 간단한 계산만 수행할 수 있습니다. 반면, 극한 계산기는 수학적으로 더 복잡한 문제에 대한 계산을 수행하기 위한 기계입니다. 이는 더욱 정확한 계산 능력과 향상된 능력을 제공합니다.
종합적으로, 극한 계산기는 매우 중요한 기술 중 하나입니다. 일부 과학적 및 수학적 문제를 해결하거나 데이터를 분석하는 경우 극한 계산기의 사용이 불가할 수 없습니다. 이러한 이유로 극한 계산기는 다른 계산기와 같은 가치가 있지 않으며, 이 기술의 발전이 계속해서 진행될 것으로 추측됩니다.
극한법칙 증명
극한은 수학에서 중요한 개념 중 하나입니다. 극한은 함수가 가까이 다가갈 때 함수 값이 어떻게 변화하는지 알려줍니다. 극한은 수학적으로 복잡한 문제를 간단하게 해결할 수 있기 때문에 수학에서 매우 중요한 개념 중 하나입니다. 극한법칙은 극한 계산을 더 쉽게 할 수 있는 규칙입니다. 이번 글에서는 극한법칙 증명에 대해 자세히 살펴보겠습니다.
극한법칙의 기본 아이디어는 함수의 근사적인 동작을 이용하는 것입니다. 특히 함수가 0에 가까이 다가갈 때 이를 근사적으로 표현하여 계산하는 방법입니다. 이러한 아이디어를 바탕으로 극한법칙을 증명할 수 있습니다.
극한법칙의 증명은 일반적으로 함수의 근사적 동작을 이용하여 이루어지며, 대략적인 접근 방법은 다음과 같습니다. 먼저 함수 f(x)의 극값과 함께 적당한 부호를 얻습니다. 그런 다음, x가 a에 가까이 다가갈 때, f(x)가 이 부호를 유지하는지 여부를 확인합니다. 이를 통해 극한을 찾을 수 있습니다.
극한법칙의 가장 간단한 형태는 다음과 같습니다. 만약 함수 f(x)의 극한이 존재하고, 어떤 상수 k가 존재하여 f(x) ≈ k x에 대해 성립한다면, 함수 f(x)의 극한은 k입니다. 이러한 극한법칙은 대학 수학 강의에서 자주 다루며, 매우 유용하게 사용됩니다.
더 나아가, 극한법칙은 다양한 형태로 확장될 수 있으며, 다음과 같은 형태로 표현할 수 있습니다.
1. 극한의 합의 법칙
lim(f(x) + g(x)) = lim(f(x)) + lim(g(x))
2. 극한의 차의 법칙
lim(f(x) – g(x)) = lim(f(x)) – lim(g(x))
3. 극한의 곱의 법칙
lim(f(x) × g(x)) = lim(f(x)) × lim(g(x))
4. 극한의 나눗셈의 법칙
lim(f(x) / g(x)) = lim(f(x)) / lim(g(x))
5. 극한의 곱셈의 법칙
lim(c f(x)) = c lim(f(x)), where c is any constant
위와 같은 법칙들은 수학에서 매우 중요하며 많은 문제들을 해결하는 데 사용됩니다.
FAQs
1. 극한법칙을 사용하는 이유는 무엇인가요?
극한법칙은 수학적으로 복잡한 문제를 간단하게 해결할 수 있기 때문에 매우 유용한 도구입니다. 극한법칙을 사용하면 대부분의 수학적 문제를 해결할 수 있으며, 더 나아가 수학에서의 기초가 됩니다.
2. 극한법칙의 증명 방법은 어떻게 되나요?
극한법칙은 함수의 근사적인 동작을 이용하여 증명합니다. 함수의 근사적인 동작은 함수의 극값을 이용하여 계산됩니다. 함수의 근사적인 동작을 파악하여 극한을 계산하면 됩니다.
3. 극한법칙은 어떻게 적용되나요?
극한법칙은 다양한 수학적 문제에서 적용됩니다. 예를 들어, 극한법칙은 수열 및 함수의 극한을 계산하는 데 사용됩니다. 또한 극한법칙은 미적분학의 개념인 미분과 적분에서 매우 중요한 역할을 합니다.
4. 극한법칙은 어떤 이론에서 사용되나요?
극한법칙은 다양한 수학 분야에서 사용됩니다. 예를 들어, 극한법칙은 해석학, 복소해석학, 적분 및 미분방정식에서 사용됩니다. 또한 극한법칙은 공학, 물리학 및 경제학과 같은 다양한 분야에서도 사용됩니다.
5. 극한법칙을 이해하기 위해서는 어떤 수학적 개념이 필요한가요?
극한법칙을 이해하기 위해서는 대수학, 함수 및 거리공간에 대한 지식이 필요합니다. 이러한 수학적 지식을 이해한 후 극한법칙을 공부하면 이해하기 쉬워집니다.
결론적으로 극한법칙은 수학에서 매우 중요하며, 적용 분야는 매우 다양합니다. 또한 극한법칙은 수학의 대부분의 분야에서 사용되므로, 수학을 공부하는 데 있어 매우 중요한 개념 중 하나입니다. 따라서, 극한법칙을 이해하고 이를 적용하는 데 큰 노력을 기울이는 것이 매우 중요합니다.
주제와 관련된 이미지 극한 공식

극한 공식 주제와 관련된 이미지 17개를 찾았습니다.

![미적분] 지수함수의 미분, 로그함수의 미분, logx 미분; 지수함수 미분 공식 증명, 로그함수 미분 공식 증명; a^x 미분 : 네이버 블로그 미적분] 지수함수의 미분, 로그함수의 미분, Logx 미분; 지수함수 미분 공식 증명, 로그함수 미분 공식 증명; A^X 미분 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAyMDAzMjVfMiAg/MDAxNTg1MDYyMTE3Mzc1.-3QnWpRn0LRIy8YmpbOcAUvNWdcGR6BVyer-dbfuL_Yg.N484bnLFGfdwZK4mOQsRp4FAYaMPQR_Ond4NwYdf9Gsg.PNG.biomath2k/image.png?type=w800)














![고3선택_미적분] 1. 수열의 극한 2) 수열의 극한의 기본성질 고3선택_미적분] 1. 수열의 극한 2) 수열의 극한의 기본성질](https://blog.kakaocdn.net/dn/UGkO7/btq3i8ijzPw/2d9Kqc03g6nA75VSjOx95K/img.png)






![미적분01 07탄] 급수와 극한의 관계 - winner 미적분01 07탄] 급수와 극한의 관계 - Winner](https://t1.daumcdn.net/cfile/tistory/2174CA395523E0F31E)
![미적분 기초 개념] 2. 초월함수 극한 공식 기초 15분 최석호 가미008 009 백미004 - YouTube 미적분 기초 개념] 2. 초월함수 극한 공식 기초 15분 최석호 가미008 009 백미004 - Youtube](https://i.ytimg.com/vi/jzQtT_dx-jE/maxresdefault.jpg)


![고3 미적분] 4강 지수함수와 로그함수의 극한 - YouTube 고3 미적분] 4강 지수함수와 로그함수의 극한 - Youtube](https://i.ytimg.com/vi/uAjBCKF5zkE/maxresdefault.jpg)


![미적분 기초 개념] 2. 초월함수 극한 공식 기초 15분 최석호 가미008 009 백미004 - YouTube 미적분 기초 개념] 2. 초월함수 극한 공식 기초 15분 최석호 가미008 009 백미004 - Youtube](https://i.ytimg.com/vi/jzQtT_dx-jE/mqdefault.jpg)




Article link: 극한 공식.
주제에 대해 자세히 알아보기 극한 공식.
- 함수의 극한(1) : 극한의 정의, 극한법칙, 극한공식(로피탈 …
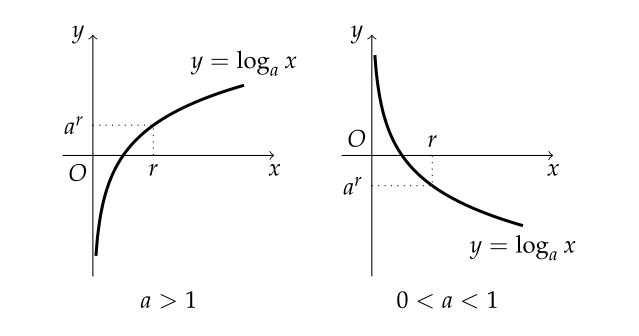
- [지수함수와 로그함수의 극한] 외워두면 좋은 기본 공식
- [미적분] 지수함수 극한 공식 증명 – 네이버 블로그 – NAVER
- 극한 – 나무위키
- 수학 공식 | 고등학교 > 함수의 극한에 대한 성질
- 삼각함수의 극한의 기본 공식 – JW MATHidea
- 수학 개념 정리/공식 : 함수의 극한, …
더보기: b1.brokengroundgame.com/krblog

