극한문제
사용자가 검색한 키워드: 극한문제 함수의 극한 문제 모음, 함수의 극한 개념, 함수의 극한 그래프 문제, 함수의 극한과 연속 문제, 함수의 극한 성질 증명, Lim 문제, 절댓값 극한, 함수의 극한 실생활
Categories: Top 70 극한문제
29. 함수의 극한 – 기본문제 & 대표유형01
여기에서 자세히 보기: b1.brokengroundgame.com
함수의 극한 문제 모음
함수의 극한은 도함수와 미분계수 등의 다른 수학적 개념과 밀접한 관련이 있습니다. 이 문제 모음에서는 함수가 어떻게 극한을 가지는지, 어떻게 극한을 구할 수 있는지 등 다양한 주제에 대해 다루고 있습니다.
이 문제 모음의 목표는 학생들이 함수의 극한에 대한 이해를 높이고, 그러한 문제들을 해결할 수 있는 능력을 기르는 것입니다.
극한 문제의 기본 원리는 다음과 같습니다. 함수의 값을 점점 더 가까이 가져가면서 극한의 값을 결정합니다. 이 기본 원리를 이해하면 다양한 극한 문제를 이해하고 해결하는 능력을 기를 수 있습니다.
함수의 극한을 제대로 이해하기 위해 먼저 함수의 정의를 살펴보아야 합니다. 함수는 변수에 대한 규칙입니다. 변수가 바뀌면 함수의 값도 바뀌게 됩니다. 따라서 함수의 극한은 변수가 점점 어떤 값으로 가까워질 때, 함수의 값이 어떻게 변화하는지를 알아내는 것입니다.
예를 들어, 함수 f(x) = x² – 1이 있을 때, x가 양수인 경우 f(x)는 양수이고, x가 음수인 경우 f(x)는 음수입니다. x가 0인 경우 f(x)는 -1이 됩니다. 이러한 경우 x가 0에 근접할 때, f(x)의 값은 언제나 -1보다 작아집니다.
이제 몇 가지 복잡한 극한 문제를 살펴보겠습니다.
극한 문제 1: lim (x² − 2x + 1) / (x − 1) (x → 1)
이 문제는 대부분의 학생들이 고민하는 문제입니다. 여기서, x가 1에 가까워질 때 x² − 2x + 1의 값은 0이 됩니다. 따라서, x − 1이 0이 아니더라도 0에 가까워지기 때문에 문제를 해결하기 위해서는 분모와 분자를 공약수 분해해야 합니다.
(x² − 2x + 1) / (x − 1) = ((x − 1)²) / (x − 1) = x − 1
따라서, lim (x² − 2x + 1) / (x − 1) (x → 1) = lim (x − 1) (x → 1) = 0
극한 문제 2: lim (sin 2x) / (3x) (x → 0)
이 문제는 sin 함수를 다뤄본 적이 있는 학생이라면 비교적 쉽게 풀 수 있습니다. 여기서, x가 0에 가까워질 때 sin 2x는 0에 가까워지기 때문에 0/0 형태가 됩니다. 따라서, 미분을 통해 문제를 해결해야 합니다.
(f(x+h) − f(x)) / h를 h → 0으로 한 값인 f'(x)를 f(x)의 미분값이라고 합니다. 이러한 개념을 이용하여, 다음과 같은 수식으로 문제를 해결할 수 있습니다.
lim (sin 2x) / (3x) (x → 0) = lim (sin2(x+h) − sin2x) / (3h) (h → 0)
= lim (sin2x cosh + sinhc cos2x − sin2x) / (3h) (h → 0)
= lim [(sin2x cosh − sin2x) / (3h)] + lim [(sinhc cos2x) / (3h)] (h → 0)
= lim [sin2x (cos h − 1) / h] / 3 + lim [sinh cos2x / 3] (h → 0)
= 2x / 3
따라서, lim (sin 2x) / (3x) (x → 0) = 2x / 3 (x → 0)
극한 문제 3: lim 2x (3 − 4x) (x → ∞)
이 문제는 x의 값이 무한대로 발산할 때 함수의 값을 구하는 문제입니다. 이러한 문제를 해결하기 위해서는 무한대의 개념을 이해해야 합니다. 무한대란 어떤 수보다 큰 수를 의미합니다.
여기서, x의 값이 무한대로 발산할 때 4x는 3보다 크고, 그 차이는 계속해서 늘어납니다. 따라서, 2x(3 − 4x)는 무한대로 발산합니다. 따라서, lim 2x (3 − 4x) (x → ∞) = ∞
이러한 문제들을 해결하기 위해서는 수학적 원리와 개념을 잘 이해하고, 극한을 구할 때 공식과 추론을 이용할 수 있어야 합니다. 이러한 것들을 연습하면서, 극한 문제 모음을 완성할 수 있습니다.
FAQs:
Q1) 극한이란 무엇인가요?
A1) 극한은 함수가 어떻게 극한을 가지는지, 어떻게 극한을 구할 수 있는지 등 다양한 주제에 대해 다루는 것입니다.
Q2) 극한 문제를 해결하기 위해 필요한 것은 무엇인가요?
A2) 극한 문제를 해결하기 위해서는 수학적 원리와 개념을 잘 이해하고, 극한을 구할 때 공식과 추론을 이용할 수 있어야 합니다.
Q3) 어떤 문제가 대표적인 극한 문제인가요?
A3) 대표적인 극한 문제로는 lim (x² − 2x + 1) / (x − 1) (x → 1)와 lim (sin 2x) / (3x) (x → 0) 등이 있습니다.
Q4) 극한 문제 모음을 푸는 것이 왜 중요한가요?
A4) 극한 문제 모음을 푸는 것은 학생들이 다양한 수학적 개념과 원리를 이해하고 분석하는 능력을 개발하는 데 큰 도움이 됩니다.
함수의 극한 개념
수학에서 함수는 다른 변수의 값에 따라 변화하는 수량을 나타내는 규칙입니다. 이러한 함수는 한 점에서 다른 점으로 연속적으로 변화하기 때문에, 함수의 극한은 매우 중요한 개념입니다.
함수의 극한은 함수에서 특정 변수가 특정 값에 접근할 때 함수가 무한히 가까워지는 지점을 나타냅니다. 이 극한은 함수가 점점 더 근접해지는 점을 가리키기 때문에 중요합니다.
함수 극한을 이해하려면, 먼저 함수의 개념부터 이해해야합니다. 함수는 변수 x의 변화에 따라 결과 y가 변화하는 규칙을 의미합니다. 수학적으로, 함수는 다음과 같은 형식으로 표현됩니다.
y = f(x)
여기서, y는 함수 f(x)의 결과를 나타내며, x는 입력 값입니다.
함수의 극한은 x가 특정 값 a로 접근할 때, 함수가 어떠한 값으로 근접하는지를 나타냅니다. 이러한 극한을 다음과 같이 표현할 수 있습니다.
lim x→a f(x)
여기서, lim은 극한을 나타내는 기호입니다. x→a는 x가 a로 접근할 때를 나타내며, f(x)는 함수입니다.
예를 들어, 함수 f(x) = 1/x의 경우를 살펴보겠습니다. 이 때, x가 점점 0으로 접근할 때 함수 f(x)의 값은 무한대로 발산하게 됩니다.
lim x→0 1/x = ∞
함수의 극한은 이와 같이 특정 값으로 접근할 때 함수의 어떠한 값으로 근접하는 지를 나타내므로, 수학에서 매우 중요한 개념 중 하나입니다.
함수의 극한은 다음과 같은 두 가지 유형으로 나눌 수 있습니다.
1. 최대 극한 (limit superior)
최대 극한은 함수의 결과가 특정 값 미만으로 떨어지는 경우, 그 값에 대한 극한입니다.
2. 최소 극한 (limit inferior)
최소 극한은 함수의 결과가 특정 값 이상으로 올라가는 경우, 그 값에 대한 극한입니다.
이러한 극한 개념은 함수의 어떠한 부분에서 최대 또는 최소 결과를 예측하는 데 매우 중요합니다.
수학에서 함수의 극한은 수열 극한과 유사한 개념입니다. 수열 극한은 수열에서 특정 값으로 접근할 때 수열의 값이 어떠한 값으로 수렴하는지를 나타내는 개념입니다. 이러한 수열 극한은 함수의 극한과 유사한 개념이기 때문에 함께 공부하면 좋습니다.
FAQs
1. 함수의 극한은 왜 중요한가요?
– 함수의 극한은 특정 값으로 접근했을 때, 함수의 결과를 예측하는 데 매우 중요합니다. 이를 이용하면 함수의 어떠한 부분에서 최대 또는 최소 결과를 예측할 수 있습니다.
2. 함수의 극한을 계산하는 방법은 무엇인가요?
– 함수의 극한을 계산하는 방법은 여러 가지가 있습니다. 수식을 이용한 계산 방법이 있으며, 그래프를 이용한 방법도 있습니다. 또한, 극한 개념을 이해하고 있는지 여부를 확인하는 문제를 푸는 방법도 있습니다.
3. 극한이 발산하는 경우, 이는 어떤 의미인가요?
– 극한이 발산하는 경우, 특정 값에 접근하였을 때 함수의 결과가 무한대로 발산하는 것을 의미합니다. 이는 함수의 결과가 점점 커질 수 있음을 나타내므로, 이를 유의해야 합니다.
4. 극한이 있는 경우, 이는 어떤 의미인가요?
– 극한이 있는 경우, 함수의 결과가 특정 값에 대해 근접하는 것을 의미합니다. 이는 함수의 결과가 어떤 범위 안에서 안정적으로 유지될 수 있음을 나타내므로, 이를 고려해야 합니다.
5. 함수의 극한 개념이 어려운 이유는 무엇인가요?
– 함수의 극한 개념은 수학적으로 복잡하며, 현실에서는 그것을 적용하는 경우가 많습니다. 따라서, 이러한 개념을 학습하는 데 다소 시간이 걸릴 수 있습니다. 그러나 이러한 개념을 이해하는 것은 중요하며, 논리적인 사고와 문제 해결 능력을 개발하는 데 도움이 됩니다.
6. 함수의 극한 개념을 활용하는 분야는 어떤 것이 있나요?
– 함수의 극한 개념은 공학, 물리학, 경제학 등 많은 분야에서 사용됩니다. 이러한 분야에서는 함수의 극한을 이용하여 복잡한 현상을 분석하고 예측하는데 활용됩니다.
7. 함수의 극한을 공부하는 방법은 무엇인가요?
– 함수의 극한을 공부하는 방법은 여러 가지가 있지만, 이해를 돕기 위해서 수식과 그림을 함께 이용하는 것이 좋습니다. 또한, 몇 가지 예제를 풀어보면서 이해도를 높일 수 있습니다. 마지막으로, 수학 문제를 해결하는 것을 중심으로 연습하는 것이 좋습니다.
함수의 극한 개념은 수학에서 중요한 개념 중 하나입니다. 이는 함수의 결과를 예측하는 데 매우 중요하며, 수학과 과학의 다양한 분야에서 활용됩니다. 함수의 극한을 이해하기 위해서는 함수의 개념부터 이해해야 하며, 계속해서 연습을 통해 높은 이해도를 얻을 수 있습니다.
주제와 관련된 이미지 극한문제

극한문제 주제와 관련된 이미지 18개를 찾았습니다.











![수학II] 2. 함수의 극한 (2) : 극한의 성질 (개념+수학문제) 수학Ii] 2. 함수의 극한 (2) : 극한의 성질 (개념+수학문제)](https://blog.kakaocdn.net/dn/vglt2/btqHG7pktb2/ioKotOVl9s3vQsCWakXnJk/img.png)





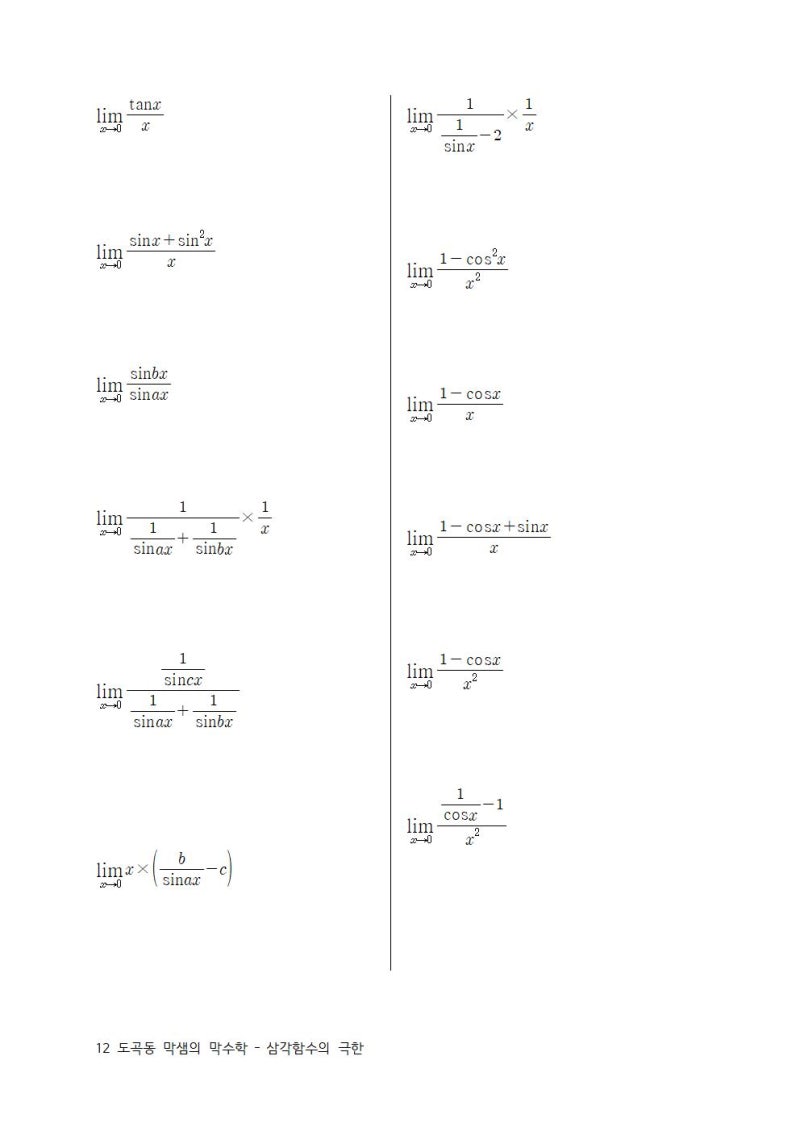




![수학공부] 미적분1 함수의 극한 - 합성함수, 가우스함수, -무한대 극한 수학공부] 미적분1 함수의 극한 - 합성함수, 가우스함수, -무한대 극한](https://t1.daumcdn.net/cfile/tistory/9988B83E5C0EA2D301)
![수학2] [심화개념] 함수의 극한 진위판정, ㄱ,ㄴ,ㄷ 문제 - YouTube 수학2] [심화개념] 함수의 극한 진위판정, ㄱ,ㄴ,ㄷ 문제 - Youtube](https://i.ytimg.com/vi/dznNr3ecBU4/maxresdefault.jpg)




![수능 속도 높이기2] 함수의 극한 문제를 최대한 빠르게 푸는 방법 - YouTube 수능 속도 높이기2] 함수의 극한 문제를 최대한 빠르게 푸는 방법 - Youtube](https://i.ytimg.com/vi/J1m1UUZf558/maxresdefault.jpg)
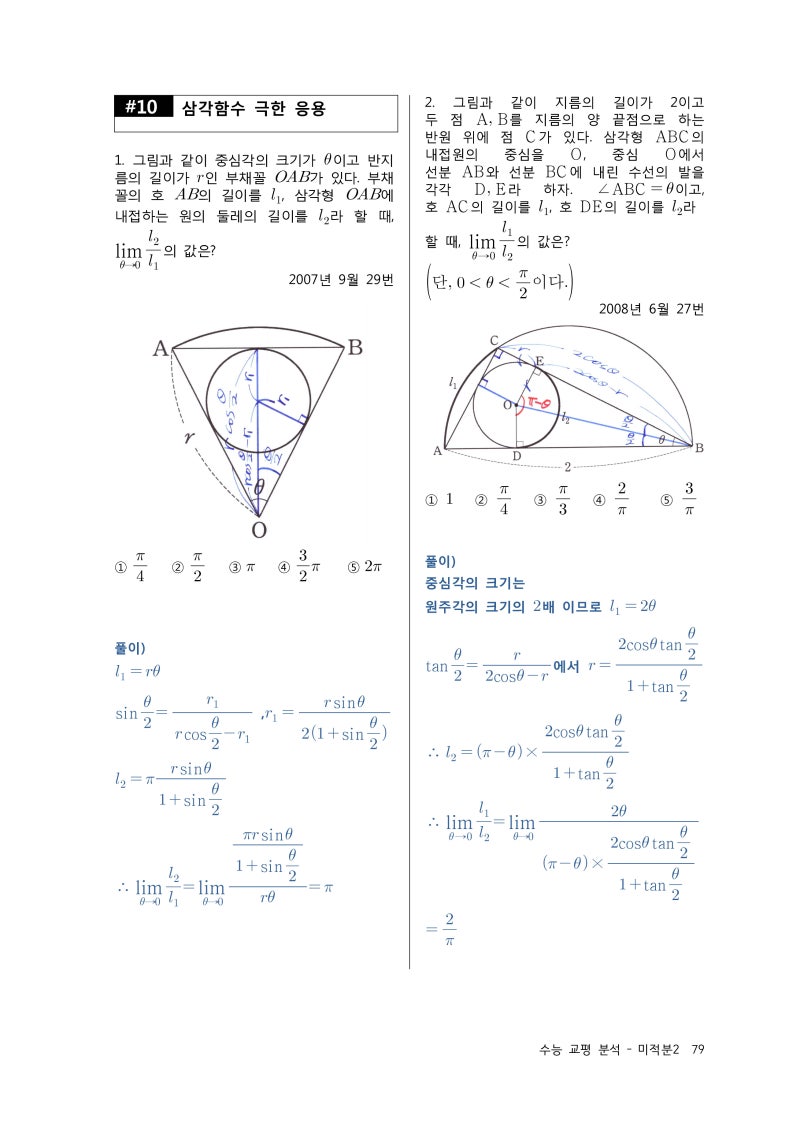


![미적분] 극한 문제 다수 - 오르비 미적분] 극한 문제 다수 - 오르비](https://s3.orbi.kr/data/file/united2/e1ac3a074ea44797bcac6c18c48f8f82.png)

![수학II] 2. 함수의 극한 (2) : 극한의 성질 (개념+수학문제) 수학Ii] 2. 함수의 극한 (2) : 극한의 성질 (개념+수학문제)](https://blog.kakaocdn.net/dn/bR1JSe/btqHGVblZR6/XndyxIjRq7JWfrRnEh4Itk/img.png)

![미적분] 삼각함수의 극한 자작 문제 - 오르비 미적분] 삼각함수의 극한 자작 문제 - 오르비](https://s3.orbi.kr/data/file/united2/f45ea2278e0c41a1b4261152c73d2d7f.png)


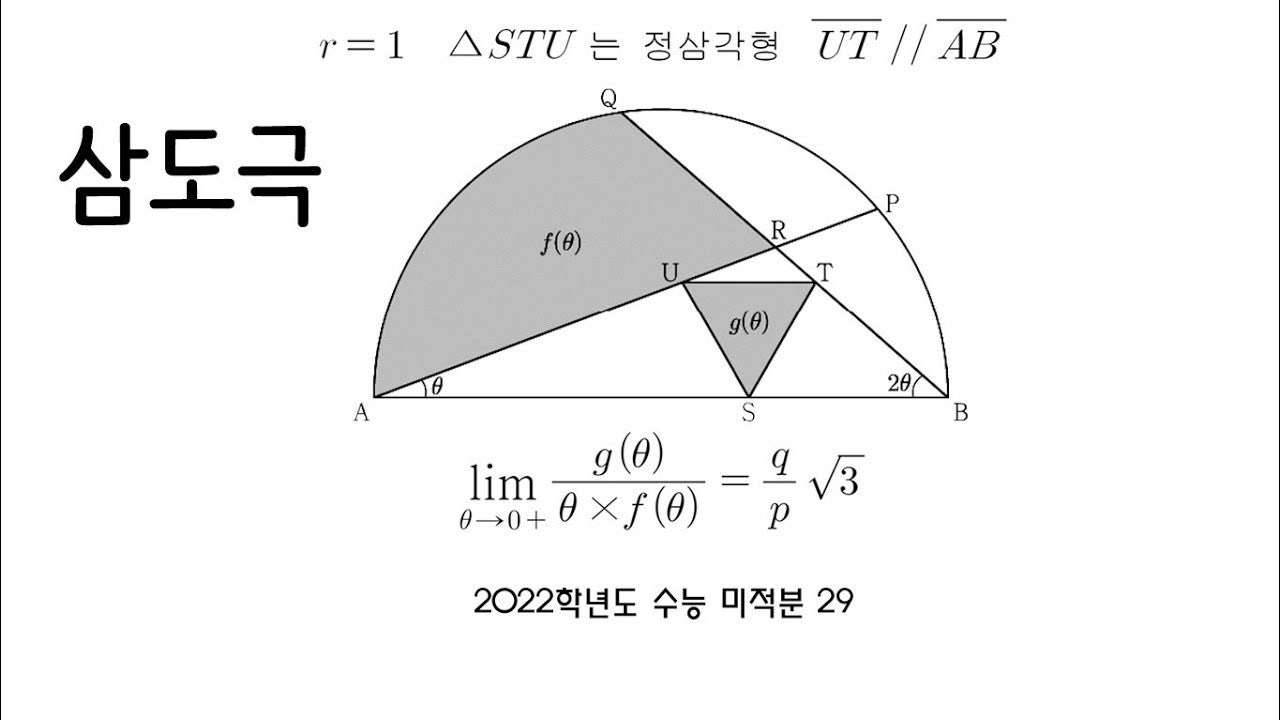

![기본개념] 함수의 극한 미정계수의 결정 기본개념] 함수의 극한 미정계수의 결정](https://t1.daumcdn.net/cfile/tistory/212B643B56913D891F)



Article link: 극한문제.
주제에 대해 자세히 알아보기 극한문제.
- 수학2 함수의 극한 단원 연습문제 (1) – 피크에듀학원
- [수학II] 2. 함수의 극한 (2) : 극한의 성질 (개념+수학문제)
- 티치온 – 문제1 : 함수의 극한 고난도 16문제 및 해설
- 극한과 연속 | 미분학 | 수학 | Khan Academy – 칸아카데미
더보기: b1.brokengroundgame.com/krblog

