근과계수의 관계
근과계수의 개념 이해
근은 다항식에서 방정식을 만족시키는 값을 의미합니다. 예를 들어 다음과 같은 2차 다항식이 있습니다.
ax² + bx + c
이 다항식의 근은 다음과 같이 표시할 수 있습니다.
(x-p)(x-q)
여기에서 p와 q는 다항식에서 x의 값을 나타냅니다. 이렇게 근은 다항식에서 근이 되는 값으로 표시될 수 있습니다.
계수는 다항식에서 변수 x에 곱해지는 상수입니다. 예를 들어 2x²에서 2는 계수입니다. 계수는 다항식에서 각 항(계수와 변수의 곱)에서 변수의 차수에 따라 다릅니다.
근과계수의 관계식 설명
근과계수의 관계식은 다음과 같습니다.
n개의 근을 가진 n차 다항식의 계수에 대한 공식은 다음과 같습니다.
aₙxⁿ + aₙ₋₁xⁿ⁻¹ + aₙ₋₂xⁿ⁻² + … + a₁x + a₀ = (x-α₁)(x-α₂)…(x-αₙ)
여기에서, a₀, a₁, a₂,…, aₙ은 다항식의 계수이며, α₁, α₂,…, αₙ은 다항식의 근입니다.
예를 들어 다음과 같은 2차 다항식이 있다고 가정해 봅시다.
x² – 6x + 8 = 0
이 식의 근은 다음과 같습니다.
(x-2)(x-4) = 0
여기에서 첫 번째 근은 2이고 두 번째 근은 4입니다. 이것은 근과계수의 관계식을 계산하는 방법을 보여 줍니다.
평면좌표에서 근과계수 나타내기
서로 다른 근은 평면좌표상에서 서로 다른 점으로 표현할 수 있습니다. 예를 들어, 다음과 같은 이차 다항식의 근을 평면좌표상에서 나타낼 수 있습니다.
x² – 4x + 3 = 0
이 문제에서 근은 1과 3입니다. 이러한 근들은 x-축에 나란히 위치해 있습니다. 따라서 평면좌표상에서 근은 (1,0)과 (3,0)으로 표현됩니다.
그러나 일반적으로 서로 다른 근은 서로 다른 위치에 있습니다. 예를 들어, 다음과 같은 2차 다항식의 경우입니다.
x² + 2x + 1 = 0
이 식의 근은 (-1,-1)입니다. 이것은 근과계수를 설명하는데 사용될 수 있는 평면좌표에서 근과계수를 나타내는 방법을 보여줍니다.
단위인수법을 이용한 근과계수의 구하는 법
근과계수를 구하는 방법 중 하나는 단위인수법을 사용하는 것입니다. 다음과 같은 공식을 이용할 수 있습니다.
단위인수법에 따라 근의 범위는 -1부터 1까지입니다. 그러나 이 방법은 단순한 방법이기 때문에 정확성이 떨어지는 경우가 있습니다.
복소수법을 이용한 근과계수의 구하는 법
복소수법은 근과계수를 구하는 더 일반적인 방법입니다. 예를 들어, 다음과 같은 2차 다항식에 대한 근과계수를 구하는 방법입니다.
x² – 6x + 8 = 0
이 식의 근은 다음과 같이 구할 수 있습니다.
x = 3 ± √1
이 글에서 √1은 숫자 1을 의미합니다. 따라서 식은 다음과 같이 수정됩니다.
x = 3 ± 1
이것은 다음과 같이 나타낼 수 있습니다.
x₁ = 4, x₂ = 2
복소수법은 근과계수를 구하는 매우 정확한 방법입니다.
다항식에서 근과계수의 관계 찾는 법
다항식에서 근과계수의 관계를 찾는 방법은 다음과 같습니다.
다항식에서 근을 찾기 위해, 일반적으로 다음과 같은 방정식을 구합니다.
ax³ + bx² + cx + d = 0
여기에서 a, b, c, d는 상수입니다.
이 식의 근은 a와 b, c와 d의 관계에서 나타납니다. 예를 들어, 만약 a와 b가 양수이고 c와 d가 음수라면, 이 식의 근은 양수입니다.
근의 개수와 계수의 관계에 대한 이해
근의 개수와 계수는 서로 밀접한 관계가 있습니다. 예를 들어, 만약 근이 3개라면, 다음과 같은 공식을 사용할 수 있습니다.
a(x-α₁)(x-α₂)(x-α₃) = a₃x³ + a₂x² + a₁x + a₀
여기에서, a는 첫 번째 근에서 x 값을 가져오도록 조정된 상수입니다. 따라서, 상수 a와 근의 개수는 상호 의존적입니다.
근과계수를 이용한 다항식의 연립방정식 풀이
다항식에서 연립방정식을 푸는 데 근과계수를 사용할 수 있습니다. 예를 들어, 다음과 같은 2차 다항식의 연립방정식을 풀어보겠습니다.
x² + y² = 1
x + y = 1
이 연립방정식의 근을 찾기 위해 우선 새로운 변수 a와 b를 도입합니다.
a = x + y
b = x² + y²
이 식을 기반으로, 연립방정식은 다음과 같이 바뀝니다.
a = 1
b = 1
이제, 근과계수를 사용하면 해를 구할 수 있습니다.
x = ½(a + √(4b – a²))
y = ½(a – √(4b – a²))
여기에서 a와 b는 위에서 지정한 변수입니다.
근과계수의 관계를 활용한 실생활 예시
근과계수의 관계는 다양한 실생활에서 사용될 수 있습니다. 예를 들어, 다음과 같은 경우입니다.
삼차방정식 근과 계수: 삼차방정식에서 근과 계수의 관계를 이용하면, 주식, 부동산 등을 포함한 다양한 경제적 문제를 해결할 수 있습니다.
이차방정식 근과 계수: 이차방정식에서 근과 계수의 관계는 과학, 기술, 경제학 등과 같은 분야에서 유용하게 사용될 수 있습니다.
두 근의 차 공식: 두 근의 차 공식은 상관분석, 확률론과 같은 분야에서 유용하게 쓰일 수 있습니다.
이차방정식 두 근의 차 공식: 이차방정식 두 근의 차 공식은 회귀분석 등에서 사용될 수 있습니다.
이차방정식 근의 합과 곱: 이차방정식 근의 합과 곱은 통계학 등에서 유용하게 활용될 수 있습니다.
두 근의 합 공식: 두 근의 합 공식은 회귀분석 등에서 사용될 수 있습니다.
이차방정식 근의 개수: 이차방정식 근의 개수는 경영, 경제학 등에서 성과 예측을 위해 사용됩니다.
삼차함수 근과 계수의 관계: 삼차함수 근과 계수의 관계는 경제학 등에서 비즈니스 분석을 위해 사용됩니다.
변곡점근과계수의 관계: 변곡점근과계수의 관계는 공학, 물리학 등에서 사용됩니다.
종합적으로 보면, 근과계수의 관계는 수학에서 중요한 부분을 차지합니다. 이것은 다항식에서 근의 개수와 계수를 설명하는 일반적인 방법입니다. 근과계수는 다양한 실습과 예제에서 유용하게 활용될 수 있습니다.
사용자가 검색한 키워드: 근과계수의 관계 삼차방정식 근과 계수, 이차방정식 근과 계수, 두 근의 차 공식, 이차방정식 두 근의 차 공식, 이차방정식 근의 합과 곱, 두 근의 합 공식, 이차방정식 근의 개수, 삼차함수 근과 계수의 관계 변곡점
Categories: Top 69 근과계수의 관계
[EBS 수학의 답] 연이차방정식 – 17. 근과 계수와의 관계(1)
여기에서 자세히 보기: b1.brokengroundgame.com
삼차방정식 근과 계수
ax^3 + bx^2 + cx + d = 0
여기서 a, b, c, d는 실수이며 a ≠ 0입니다. 삼차 방정식의 근을 구하는 것은 수학에서 중요한 문제 중 하나입니다. 이 문제를 해결하기 위해서는 삼차 방정식의 계수와 근 사이에 어떤 관계가 있는지 이해해야 합니다.
삼차 방정식의 계수
삼차 방정식의 계수는 처음에 주어진 방정식에서 x의 지수에 해당하는 각 항의 계수를 말합니다. 따라서 위의 방정식에서 계수는 a, b, c, d입니다. 삼차 방정식의 근을 구하는 데는 계수들을 이용하는 여러 가지 방법이 있습니다.
한 가지 방법은 Vieta의 공식을 이용하는 것입니다. Vieta의 공식은 삼차 방정식의 근과 계수 사이의 관계를 나타내는 공식입니다. Vieta의 공식에 의하면, 삼차 방정식 ax^3 + bx^2 + cx + d = 0의 근이 x1, x2, x3일 때, 다음과 같은 식이 성립합니다.
x1 + x2 + x3 = -b/a
x1x2 + x1x3 + x2x3 = c/a
x1x2x3 = -d/a
위의 식에서 볼 수 있듯이, 삼차 방정식의 계수가 근과 어떤 관계를 가지는지 알면 근을 구하는데 유용한 정보를 얻을 수 있습니다.
삼차 방정식의 근
삼차 방정식은 세제곱의 항이 있기 때문에 근이 세 개입니다. 이 세 개의 근은 모두 실수일 수도 있고, 복소수일 수도 있습니다. 따라서 삼차 방정식의 근을 구하는 과정에서는 복소수와 관련된 개념을 이해해야 합니다.
유리근과 무리근
삼차 방정식의 근은 유리근과 무리근으로 나뉩니다. 유리근은 분모가 없는 유리수인 근으로, 예를 들어 √2는 유리수가 아니지만 1/√2은 유리수입니다. 무리근은 유리수가 아닌 근으로, 예를 들어 √2는 무리수입니다.
삼차 방정식의 근이 모두 유리근인 경우는 드뭅니다. 대부분의 경우 삼차 방정식의 근은 무리근 혹은 복소수근입니다. 따라서 삼차 방정식의 근을 구하는 과정에서는 무리근과 복소수근을 다룰 수 있어야 합니다.
복소수와 켤레복소수
복소수는 a + bi와 같은 형태를 가지는 수로, i는 양의 제곱근 -1을 나타냅니다. 이 때, a는 실수부, b는 허수부라고 합니다. 삼차 방정식의 근이 복소수인 경우, 켤레복소수 개념을 이용해 근을 구할 수 있습니다.
켤레복소수는 a – bi와 같은 형태를 가지는 수로, 실수부는 동일하지만 허수부의 부호만 다릅니다. 따라서 복소수 z와 켤레복소수 z*의 합은 실수입니다. 삼차 방정식의 근이 복소수인 경우, 코사인 법칙과 삼각함수를 이용해 켤레복소수를 구할 수 있습니다.
FAQs
Q: 삼차 방정식의 해 구하는 방법은 무엇인가요?
A: 삼차 방정식의 풀이 방법에는 여러 가지가 있습니다. 한 가지 방법은 Vieta의 공식을 이용하여 근과 계수 사이의 관계를 이용하는 것입니다. 또 다른 방법은 공식을 이용하여 근을 구하는 것입니다. 이 공식은 삼차 방정식의 계수와 상수항을 이용하여 해를 구하는 것입니다. 이때, 유리근과 무리근, 복소수근에 따라서 계산법이 다릅니다.
Q: 삼차 방정식에서 구한 실근과 복소근의 개수는 어떻게 구할까요?
A: 삼차 방정식에서 실근과 복소근의 개수는 “판별식”을 이용해서 구할 수 있습니다. 판별식은 방정식의 계수들로 이루어진 다항식이며, 일반적으로 $\Delta$ (Delta)로 표기합니다. 삼차방정식의 판별식은 다음과 같이 정의됩니다.
$\Delta = b^2 – 4ac$
여기서, b, c, a는 방정식의 계수입니다. 이 때, $\Delta$가 0보다 큰 경우, 2개의 실근이 존재합니다. $\Delta$가 0인 경우, 중근이 하나 있습니다. $\Delta$가 0보다 작은 경우, 2개의 복소근이 존재합니다.
Q: 삼차 방정식에서 근사적인 해를 구하는 방법이 있나요?
A: 삼차 방정식에서 근사적인 해를 구하는 방법에는 뉴튼랩슨법 (Newton-Raphson method)와 이분법 (Bisection method) 등이 있습니다. 이분법은 시간이 오래 걸리고 근사적인 값을 일일이 찾아야 하지만, 뉴튼랩슨법은 보통 이보다 빠르고 정교한 값들을 찾아낼 수 있습니다.
이차방정식 근과 계수
이차방정식은 다음과 같은 형식을 가진 방정식이다.
ax² + bx + c = 0
여기서 a, b, c는 상수이며 a ≠ 0이다.
이차방정식은 최대 2개의 해를 갖는다. 이를 이차방정식의 근이라고 부른다.
이차방정식의 근은 다음과 같은 공식을 이용하여 구할 수 있다.
x = (-b ± √(b² – 4ac)) / 2a
여기서 ±는 양수와 음수를 모두 포함한 것이다.
이차방정식의 계수는 각 항의 계수이다. 즉, 위의 방정식에서 a, b, c가 이차방정식의 계수이다.
이차방정식 근과 계수는 다양한 문제에서 사용되며, 중요한 개념이다. 이어서 더 자세히 알아보자.
이차방정식 근
이차방정식은 최대 2개의 해를 갖는다. 이를 이차방정식의 근이라고 한다.
근의 개수는 이차방정식의 판별식인 D = b² – 4ac를 이용하여 구할 수 있다.
1) D > 0인 경우
D > 0이면 이차방정식은 서로 다른 두 실근을 갖는다.
예를 들어, x² – 3x + 2 = 0은 x = 1, 2라는 두 개의 서로 다른 실근을 갖는다.
2) D = 0인 경우
D = 0이면 이차방정식은 중근을 갖는다.
예를 들어, x² – 4x + 4 = 0은 x = 2라는 중근을 갖는다.
3) D < 0인 경우 D < 0이면 이차방정식은 실근을 갖지 않는다. 하지만, 허근을 갖는다. 이 경우에는 복소수를 이용하여 해를 구한다. 예를 들어, x² + 2x + 2 = 0은 해가 없다. 하지만, x = -1 + i, -1 - i라는 두 개의 복소근을 갖는다. 여기서 i는 허수 단위이다. 이차방정식 계수 이차방정식의 계수는 각 항의 계수이다. 위의 방정식에서 a, b, c가 각각 이차항, 일차항, 상수항의 계수이다. 이차방정식의 계수를 이용하여 이차방정식 근을 구할 수 있다. 또한, 이차방정식의 계수를 이용하여 이차방정식의 특성을 파악할 수 있다. 예를 들어, 이차방정식의 계수와 근의 관계는 다음과 같다. 1) 이차방정식이 ax² + bx + c = 0일 때, a > 0이면, 이차방정식은 위로 볼록한 그래프를 그린다.
a < 0이면, 이차방정식은 아래로 볼록한 그래프를 그린다. 2) 이차방정식이 x² - 6x + 8 = 0일 때, 해를 구하는 공식을 이용하여 x = 2, 4를 구할 수 있다. 계수 a가 1이고 해가 2와 4이므로, 이차방정식은 위로 볼록한 그래프를 그린다. 3) 이차방정식이 2x² + 3x - 4 = 0일 때, 해를 구하는 공식을 이용하여 x ≈ -1.46, x ≈ 1.08을 구할 수 있다. 계수 a가 양수이므로, 이차방정식은 위로 볼록한 그래프를 그린다. FAQs 1) 이차방정식에서 a는 0이 될 수 있나요? 이차방정식에서 a는 0이 될 수 없습니다. 이는 이차방정식의 특성으로, a가 0이면 일차방정식이 되기 때문입니다. 2) 이차방정식의 근은 최대 몇 개까지 있을 수 있나요? 이차방정식의 근은 최대 2개까지 있을 수 있습니다. 3) 이차방정식의 근은 실근과 복소근이 있을 수 있다는데, 복소근이 무엇인가요? 복소근은 허수를 포함한 수입니다. 이는 이차방정식의 판별식인 D가 음수일 때 나타납니다. 4) 이차방정식의 계수를 이용하여 이차방정식의 특성을 어떻게 파악할 수 있나요? 이차방정식의 계수를 이용하여 이차방정식이 위로 볼록한 그래프를 그리는지 아래로 볼록한 그래프를 그리는지 파악할 수 있습니다. 또한, 계수를 이용하여 근의 개수를 예측할 수도 있습니다. 5) 이차방정식의 공식은 어떻게 구할 수 있나요? 이차방정식의 공식은 완전 제곱 공식을 이용하여 유도할 수 있습니다. 이는 교과서에서 자세히 설명되어 있으니 참고하시기 바랍니다.
주제와 관련된 이미지 근과계수의 관계
![[EBS 수학의 답] 연이차방정식 - 17. 근과 계수와의 관계(1) [EBS 수학의 답] 연이차방정식 - 17. 근과 계수와의 관계(1)](https://b1.brokengroundgame.com/wp-content/uploads/2023/06/hqdefault-1760.jpg)
근과계수의 관계 주제와 관련된 이미지 36개를 찾았습니다.
![방정식] 이차방정식 근과 계수 관계 공식 유도: 이차방정식 두 근의 합, 두 근의 곱, 두 근의 비; 이차방정식 근과 계수의 관계 : 네이버 블로그 방정식] 이차방정식 근과 계수 관계 공식 유도: 이차방정식 두 근의 합, 두 근의 곱, 두 근의 비; 이차방정식 근과 계수의 관계 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAyMDA0MDVfNzYg/MDAxNTg2MDEzNzc3Nzc2.MtvGkai9RQIihZfCdlUNnkxJc6EW-9sbLbPdE3Uy0vQg.YHmGWNs_0OBDBh_TfPEkUxux0QhD-vN6t_s0s4u7pcIg.PNG.biomath2k/image.png?type=w800)








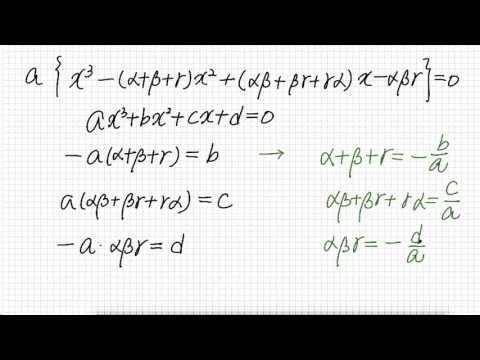

![고2수학 수1] [로그] 로그와 이차방정식의 근과 계수의 관계 [수포자 구원 프로젝트] (만수동 토모수학학원) : 네이버 블로그 고2수학 수1] [로그] 로그와 이차방정식의 근과 계수의 관계 [수포자 구원 프로젝트] (만수동 토모수학학원) : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAyMDAzMTZfMTk1/MDAxNTg0MzU5MDc1OTgy.JA-EmsZfruot71jhuzC_6jESsqHlFKl5bkLZLXl-ib8g.mXc1McK-uH_oh61kHM_zlrQa0OUns9TA0f_USGeCVmMg.PNG.10baba/%EB%A1%9C%EA%B7%B8%EC%99%80_%EC%9D%B4%EC%B0%A8%EB%B0%A9%EC%A0%95%EC%8B%9D%EC%9D%98_%EA%B7%BC%EA%B3%BC_%EA%B3%84%EC%88%98%EC%9D%98_%EA%B4%80%EA%B3%84.png?type=w800)
![수학2] 삼차함수의 접선과 근과 계수의 관계 #1 : 네이버 블로그 수학2] 삼차함수의 접선과 근과 계수의 관계 #1 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAyMDA5MTZfMTkx/MDAxNjAwMjA1MzI0OTY0.UjQenn5zHq6FWNh3DZn0tFDTq3u9bl0apxU5Zlnw9Xog.rcCcwc-G0w_fxvSbJIO3H89ZJGmxV91FYHVlb_6MmeMg.PNG.tiemath/2013%ED%95%99%EB%85%84%EB%8F%846%EC%9B%94%ED%8F%89%EA%B0%80%EC%9B%90_%ED%95%B4%EC%84%A4.png?type=w800)

![corestudy] 지수함수(24)-지수방정식(근과 계수의 관계) - YouTube Corestudy] 지수함수(24)-지수방정식(근과 계수의 관계) - Youtube](https://i.ytimg.com/vi/fXOeP5PDIjE/maxresdefault.jpg)
![Ⅱ 방정식과 부등식 ] [ 06. 이차방정식의 근과 계수의 관계 ] Ⅱ 방정식과 부등식 ] [ 06. 이차방정식의 근과 계수의 관계 ]](https://img.youtube.com/vi/vqDWPE5AiVM/hqdefault.jpg)


![수학설명] 수학(상) 근의 공식, 근과 계수와의 관계 : 네이버 블로그 수학설명] 수학(상) 근의 공식, 근과 계수와의 관계 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAxODEwMjJfMjkw/MDAxNTQwMTgzMzAzMTcy.8byTArLB6YYRYGr_5cdNRLYAEIFf92GfOGGdw3iyPTog.VGviC3DCoeE5nkzpJsrNVD8t3KudZo2vzMLTwGpML9Ug.JPEG.jjangting/%EA%B7%BC%EC%9D%98%EA%B3%B5%EC%8B%9D.jpg?type=w800)


![수(상)][LV 1] 22강. 이차방정식_근과 계수의 관계 - YouTube 수(상)][Lv 1] 22강. 이차방정식_근과 계수의 관계 - Youtube](https://i.ytimg.com/vi/v8OTdbhKAB8/maxresdefault.jpg)




![손T네 수학맛집 - 짤강시리즈] 손대장이 알려주는 N차 방정식의 근과 계수와의 관계 - Viete's Theorem - YouTube 손T네 수학맛집 - 짤강시리즈] 손대장이 알려주는 N차 방정식의 근과 계수와의 관계 - Viete'S Theorem - Youtube](https://i.ytimg.com/vi/O-02GC13vow/maxresdefault.jpg)

Article link: 근과계수의 관계.
주제에 대해 자세히 알아보기 근과계수의 관계.
- 이차방정식 근과 계수의 관계 – 네이버 블로그
- [5분 고등수학] 이차방정식의 근과 계수의 관계
- 근과 계수의 관계_이차방정식 – 켄아담스
- 이차방정식 근의 공식 말고, 창의적인 풀이 방법 / 근과 계수와의 …
- [수학상] 이차방정식의 근과 계수와의 관계, 두근의 … – YouTube
- 근과 계수와의 관계 – 모든 수학
- 비에트의 정리 – 나무위키
더보기: b1.brokengroundgame.com/krblog

