근의 공식 만든 사람
1. 근의 공식의 개발자
알콰리즈미는 8세기 아랍의 수학자로, 가능성 있는 매우 다양한 분야에서 일했다. 그는 우리가 오늘날 사용하는 ‘알고리즘’이라는 용어를 만든 사람으로도 알려져 있다. 그러나 그의 가장 중요한 업적 중 하나는 근의 공식의 발명이다. “Hisab al-Jabr w’al-Muqabala”라는 책에서 알콰리즈미는 제곱과 선형항, 상수항 등을 포함한 이차방정식의 근을 구하는 방법과 함께 근의 공식을 제시한다.
2. 구체적인 개발 과정
근의 공식은 오랜 세월동안 다양한 형태로 발전해왔다. 이는 모두 각기 다른 수학자들에 의해 발전한 공식으로, 중동 지역에서 발전하며 유럽과 미국으로 전파되었다.
알콰리즈미의 근의 공식은 8세기 이슬람 미국에서 발명되었다. 그 후 16세기 이모토 에키도는 3차 방정식 근의 공식을 발명하였으며, 이 공식은 내적법 등과 함께 나라별로 타산지존한 분파가 만들어졌다. 이후 프랑스 수학자 프랑수아 비에트 (Francois Viète)는 대수 최신 기술을 통해 페랴마의 방정식의 해를 찾아낼 수 있는 알고리즘을 발명하였다. 이후 레네 데카르트(Rene Descartes)는 각 항들을 제곱항과 선형항으로 나누어 표시하는 데 힘써, 이를 바탕으로 근의 공식을 개선했다. 그러나 정확한 근을 찾는 방법으로 사용되는 역할은 전략적 피트니(Pythagoras)와 유클리드(Euclid), 그리고 후에 베러트(Barrow)와 뉴턴(Newton)등의 수학자들이 개발한 다양한 방법들특히, 인터내셔널 타산지존한 방식을 개발한 뉴턴의 경우 알고리즘과 이론적 분석에서 압도적 성과를 내었다.
3. 근의 공식의 응용 분야
근의 공식은 수많은 분야에서 응용된다. 예를 들어, 기계 학습에서 이차원 또는 삼차원 공간상의 데이터 분석에 사용될 수 있다. 또한 이를 응용하여 다른 분야에서 유용하게 사용될 수 있으며, 예를 들면 경제학에서는 수요와 공급 그래프를 구성하여 가격 변동을 예측하는 데에 사용되기도 한다. 그리고 미적분학에서는 미분법과 함께 사용되어 곡선의 최저/최고점을 미리 예측할 수 있다.
4. 근의 공식이 미치는 영향
근의 공식은 대수학, 수학, 공학 그리고 경제학 등 다양한 분야에서 널리 활용되고 있으며, 또한 컴퓨터 과학 등 현대 기술 분야에서도 중요한 역할을 한다.
5. 개발자의 이력과 업적
알콰리즈미는 8세기 이슬람의 수학자로, 근의 공식 외에도 다양한 분야에서 활동하였다. 그는 알고리즘의 개념을 처음으로 정립하였으며 이 개념은 컴퓨터 과학에서 매우 중요한 개념 중 하나이다. 그리고 그의 업적과 이력은 훌륭한 교육자로 남아 더욱 높은 평가를 받고 있으며 기억하고 있어야 할 두 개의 학명을 가지고 있다.
6. 근의 공식의 발전 방향
현재까지 수학에서의 발전은 더 이상 근의 공식과 같은 개념에 의존하지 않고 있다. 그러나 이 공식은 알고리즘 및 숫자 계산에 대한 일반적인 이해를 높이는 데에 큰 역할을 할 수 있다. 또한 현재는 더욱 나은 방법과 기술에 의존해 다양한 작업과 분야에서 활용되고 있다.
7. 근의 공식의 활용 가능성
알콰리즈미의 근의 공식 외에도, 이차방정식과 관련된 수학 인물들이 근의 공식을 발전시켰다. 그 중 언급해볼만한 사람은 이차방정식의 개념을 처음으로 만든 바바라 바밀로(Baba Barbara)와 16세기 이모토 에키도가 있다. 또한 브라마굽타(Brahmagupta)는 여러 가지 알고리즘들에 대해 작성하였으며, 그 중 하나는 이차방정식의 근을 찾는 방법이다. 이 외에도 다양한 역사적인 인물들이 근의 공식과 관련된 알고리즘을 개발하였다.
FAQs
Q: 근의 공식이란 무엇인가요?
A: 근의 공식은 다항식의 근을 계산하는 공식입니다.
Q: 근의 공식은 어떻게 발달해왔나요?
A: 근의 공식은 알콰리즈미를 비롯한 수많은 수학자들에 의해 발전해왔습니다. 이 공식은 중동 지역에서 발전하며 유럽과 미국으로 전파되었습니다.
Q: 근의 공식은 어떤 분야에서 사용될 수 있나요?
A: 근의 공식은 수학, 공학, 경제학 등 다양한 분야에서 사용될 수 있습니다.
Q: 근의 공식은 미래에도 중요한 역할을 할까요?
A: 현재까지 수학에서의 발전은 더 이상 근의 공식과 같은 개념에 의존하지 않고 있습니다. 그러나 이 공식은 알고리즘 및 숫자 계산에 대한 일반적인 이해를 높이는 데에 큰 역할을 할 수 있습니다.
사용자가 검색한 키워드: 근의 공식 만든 사람 알콰리즈미 근의 공식, 이차방정식 관련 수학자, 3차 방정식 근의 공식, 복원과 대비의 계산, 알고리즘 수학자, 브라마굽타 근 의 공식, 이차방정식의 역사, 근의 공식 위키
Categories: Top 97 근의 공식 만든 사람
지면 실업자가 되는 수학 배틀 : 허수는 어떻게 만들어 졌을까?
여기에서 자세히 보기: b1.brokengroundgame.com
알콰리즈미 근의 공식
알콰리즈미 근의 공식 소개
알콰리즈미 근의 공식은 다음과 같습니다.
√ax^2 + bx + c = (-b ± √(b^2 – 4ac)) / 2a
여기서 a, b, c는 각각 0이 아닌 실수이며, x는 변수입니다. 이 공식은 일반적으로 이차방정식에서 근을 구할 때 사용됩니다. 이차방정식은 ax^2 + bx + c = 0으로 표현되며, 이때 a, b, c는 각각 계수이며, x는 미지수입니다.
이제 이차방정식으로 예를 들어 알콰리즈미 근의 공식을 사용해보겠습니다.
예를 들어, x^2 + 6x + 8 = 0인 이차방정식이 있다고 가정해봅시다. 이때, a = 1, b = 6, c = 8입니다. 이 값을 공식에 대입하면 다음과 같습니다.
x = (-6 ± √(6^2 – 4(1)(8))) / 2(1)
= (-6 ± √(36 – 32)) / 2
= (-6 ± √4) / 2
= (-6 ± 2) / 2
이렇게 구한 결과 x는 -4 또는 -2가 됩니다.
알콰리즈미 근의 공식의 원리
알콰리즈미 근의 공식은 이차방정식에서 근을 구하기 위해 사용됩니다. 이 공식은 이차방정식으로부터 근의 공식을 유도하는 것이 아니라, 완전한 제곱 형태로 변환한 후, 간단한 계산식으로 계산하는 방식입니다. 이 방식은 계산을 더욱 쉽게 수행할 수 있도록 하며, 오류를 줄이는 데에도 도움을 줍니다.
알콰리즈미 근의 공식을 사용하면, 이차방정식의 두 근을 구할 수 있습니다. 이때, 이차방정식에서 b^2 – 4ac를 계산하는 과정에서 나온 값의 제곱근을 사용해서 근을 구하는 것이 특징입니다. 이론적으로는 완전한 제곱 형태로 변환이 불가능한 경우에는 본 공식을 사용할 수 없습니다. 따라서 이 경우 다른 방법을 찾아야 합니다.
FAQs
Q: 알콰리즈미 근의 공식이란 무엇인가요?
A: 알콰리즈미 근의 공식은 제곱근을 구하는 방법 중 하나로, 일반적인 제곱근의 계산과 달리 근과 상수의 곱 계산을 수행하는 방식으로 제곱근을 더욱 쉽게 계산할 수 있도록 도와줍니다.
Q: 알콰리즈미 근의 공식은 어떻게 사용되나요?
A: 알콰리즈미 근의 공식은 이차방정식에서 근을 구하기 위해 사용됩니다.
Q: 알콰리즈미 근의 공식이 어렵게 느껴지는데, 사용하는 이유는 무엇인가요?
A: 알콰리즈미 근의 공식은 이차방정식의 근을 더 쉽게 구할 수 있도록 도와주는 방식입니다. 이 공식은 일반적인 제곱근의 계산 방식과 달리 근과 상수의 곱 계산을 수행하는 방식으로 제곱근을 더욱 쉽게 계산할 수 있도록 하기 때문에 사용합니다.
Q: 알콰리즈미 근의 공식의 원리는 무엇인가요?
A: 알콰리즈미 근의 공식은 이차방정식을 완전한 제곱 형태로 변환한 후, 간단한 계산식으로 계산하는 방식입니다. 이 방식은 계산을 더욱 쉽게 수행할 수 있도록 하며, 오류를 줄이는 데에도 도움을 줍니다.
Q: 알콰리즈미 근의 공식을 사용할 때 주의할 점은 무엇인가요?
A: 알콰리즈미 근의 공식을 사용할 때는 b^2 – 4ac가 0보다 큰 값이어야 합니다. 만약 이 값이 0보다 작다면, 이차방정식에 실근이 없는 경우입니다. 또한 계산 시 소수점 및 음수 처리에 유의해야합니다.
종합적으로, 알콰리즈미 근의 공식은 이차방정식에서 근을 구하기 위한 유용한 도구입니다. 이 공식을 사용하면, 빠르게 근을 구할 수 있으며, 본인의 수학적 능력을 키울 수 있습니다. 사용할 때 주의사항을 잘 숙지하여, 정확하게 계산할 수 있도록 합시다.
이차방정식 관련 수학자
이차방정식과 관련된 대부분의 과학자나 수학자는 현대의 전설적 수학자 중 한 명인 Pierre de Fermat 일 것이다. 그는 1637 년에 “Fermat의 마지막 정리”라고 알려진 이론을 제안한 과학자 중 하나였다. 그는 간단한 이차방정식에 관한 문제를 제시하였고, 이 문제는 150 년 동안 풀리지 않았다.
이차방정식과 관련하여 다른 중요한 성취를 달성한 몇몇 다른 수학자들도 있다. 이 방정식에 대한 답을 찾기 위해 애쓴 노력으로 유명한 수학자 중 하나는 오일러 (Euler)이다. 그는 이차방정식을 풀기 위해 수학에서 새로운 형태의 함수를 연구하였으며, 이 함수는 지금까지 오일러 함수로 알려져 있다. 오일러 함수는 많은 인터넷 암호학에서 중요한 역할을 담당하고 있으므로 이 함수가 사실상 이차방정식 및 소수 이론과 관련이 있다는 것이 명백하다.
그러나 많은 수학자들이 이차방정식의 해결 방법을 찾았다. 기원전 700 년에 살았던 중국의 수학자 제가 성 (Chang Qu)은 이제 “성의 공식”으로 알려진 공식을 찾아 이차방정식의 해를 구하였다. 이 공식은 천하대전에 실렸으며, 이를 사용하여 특정 형태의 이차방정식을 해결할 수 있다.
자카래스 (Jacobi)는 1800년대 후반에 이차방정식의 이론을 깊이 연구한 몇 명 중 한 명이다. 그는 이차방정식의 해결을 위해 고전적인 방법을 사용하지 않았으며, 대신에 새로운 방법과 개념을 도입하였다. 이를 통해 많은 이차방정식 문제를 해결할 수 있었다.
그러나, 이차방정식의 해결 방법이 지금까지도 아직 새로운 분야에서 연구되고 있음에도 불구하고, 현재 적용되고 있는 흔한 이차방정식 해결 방법은 근의 공식이다. 이 공식은 이차방정식의 해를 찾는 효과적인 방법이며, 이 때 정확한 해를 얻을 수 있다.
FAQs
1. 이차방정식이란 무엇인가?
– 이차방정식은 ax²+bx+c 형태의 방정식을 뜻한다. 그 중에서 a가 0이 아니면 이차방정식이라고 한다.
2. Pierre de Fermat이 이차방정식과 관련하여 무엇을 연구하였나요?
– Fermat은 1637 년에 이차방정식의 간단한 문제를 제시하였으며, 이 문제는 150 년 동안 풀리지 않았다. 이를 “Fermat의 마지막 정리”라고 한다.
3. 이차방정식을 해결하기 위한 가장 흔한 방법은 무엇인가요?
– 현재 적용되고 있는 흔한 이차방정식 해결 방법은 근의 공식이다.
4. 자카래스가 이차방정식 연구에 어떤 차별화된 방법을 사용했나요?
– 자카래스는 이차방정식 해결에 대해 고전적인 방법을 사용하지 않았으며, 대신 새로운 방법과 개념을 도입하여 많은 이차방정식 문제를 해결하였다.
5. 오일러 함수가 무엇인가요?
– 오일러 함수는 이차방정식을 풀기 위해 수학에서 새로운 형태의 함수를 연구하였으며, 이 함수는 지금까지 오일러 함수로 알려져 있다. 이 함수는 많은 인터넷 암호학에서도 중요한 역할을 담당하고 있다.
6. 이차방정식의 해결 방법이 지금까지도 연구되고 있나요?
– 예, 이차방정식의 해결 방법은 지금까지도 여러 연구 분야에서 연구되고 있다.
3차 방정식 근의 공식
3차 방정식은 다음과 같은 형태의 방정식이다.
ax³ + bx² + cx + d = 0
여기서 a, b, c, d는 실수 계수이며, a ≠ 0 이다. 3차 방정식의 해를 구하는 것은 대개 매우 어려운 문제이다. 따라서 3차 방정식의 해를 찾기 위해 사용되는 공식이 바로 3차 방정식 근의 공식이다.
3차 방정식 근의 공식은 다음과 같다.
x = [-b ± √(b² – 4ac – 3ad²) ] / 3a
이 공식에서 √(b² – 4ac – 3ad²)은 구해야 할 근의 값이다. 만약 이 값이 실수이면, 방정식의 해는 두 개가 나오며, 복소수일 경우 해는 세 개가 된다.
3차 방정식 근의 공식은 그 자체로 매우 복잡한 형태를 가지고 있으며, 이를 사용하는 것도 매우 까다롭다. 따라서 대부분의 경우 프로그래밍 언어나 전문적인 계산기를 이용하여 3차 방정식의 근을 구한다.
FAQs
Q: 3차 방정식 근의 공식은 어떻게 유도되었나요?
3차 방정식 근의 공식은 세기 전 유럽에서 등장한 이태리 수학자 카르다노(Cardano)와 프랑스 수학자 페루(Girolamo Cardano, Scipione del Ferro) 그리고 휘트니(알베르트 휘트니, 채지성)가 연구한 내용으로, 빈 자리의 제곱수를 더하는 방법 등 여러 가지 방법론을 조합하여 유도되었습니다.
Q: 3차 방정식 근의 공식을 사용할 때, 어떤 주의점이 있나요?
3차 방정식 근의 공식은 매우 복잡하기 때문에 사용할 때에는 다음과 같은 주의점이 있습니다.
1. 분모가 0이 되는 경우를 피해야 합니다.
2. 제곱근의 계산에서 오차가 발생할 가능성이 있습니다.
3. 복소수 값이 나올 수 있으므로, 복소수 처리에 주의해야 합니다.
Q: 3차 방정식의 해를 구하는 방법에는 어떤 것이 있나요?
3차 방정식의 해를 구하는 방법에는 다음과 같은 것들이 있습니다.
1. 그래프로 나타내어 근을 구하는 방법
2. 뉴턴 방법(Newton’s method)을 사용하여 근을 구하는 방법
3. 제안한 근을 다시 대입하여 해를 구하는 방법
4. 3차 방정식의 계수를 이용하여 근의 범위를 고려하여 해를 구하는 방법
이 중, 3차 방정식 근의 공식은 3번 방법을 사용하여 유도되었습니다.
Q: 3차 방정식 근의 공식은 4차, 5차 방정식에도 사용이 가능한가요?
아니요. 3차 방정식 근의 공식은 3차 방정식에서만 사용이 가능하며, 4차 방정식 이상에서는 다른 방법을 사용하여야 합니다.
Q: 3차 방정식 근의 공식을 사용하면서 발생할 수 있는 문제에 대해서 알려주세요.
1. 분모가 0이 되는 경우
3차 방정식 근의 공식에서 분모 부분에는 3a가 곱해진 형태로 되어 있습니다. 따라서 a가 0이 되는 경우에는 분모가 0이 되어 에러를 발생시키기 때문에 주의해야 합니다.
2. 실수로 나타낼 수 없는 근이 나오는 경우
3차 방정식 근의 공식을 사용할 때, 제곱근의 값이 음수일 경우 실수로 나타낼 수 없는 복소수 근이 나올 수 있습니다. 따라서 근이 복소수인 경우 적절한 처리를 해주어야 합니다.
3. 제곱근 계산 오차
3차 방정식 근의 공식에서는 제곱근을 사용하는 부분이 포함되어 있어, 제곱근 계산 오차가 발생할 수 있습니다. 따라서 정확성을 보장하려면 수학 라이브러리 등을 사용하기도 합니다.
4. 복잡한 계산
3차 방정식 근의 공식은 자체로 복잡한 형태를 가지고 있기 때문에, 계산자체가 어렵고 오류가 발생하기 쉽습니다. 따라서 프로그래밍 언어나 전문적인 계산기를 이용하여 근을 구하는 것이 보편적인 방식입니다.
Q: 3차 방정식 근의 공식을 사용하여 문제를 풀 때, 어떤 식으로 접근해야 할까요?
3차 방정식 근의 공식을 사용하여 문제를 풀 때에는, 다음과 같은 절차를 따르는 것이 좋습니다.
1. 방정식의 계수 a, b, c, d를 구합니다.
2. 3차 방정식 근의 공식을 적용하여 근의 값을 구합니다.
3. 구한 근의 값을 원래 방정식에 다시 대입하여 정확성을 검증합니다.
4. 근의 개수와 근의 형태에 따라서 출력을 조절합니다.
이렇게 하면 3차 방정식 근의 공식을 보다 효과적으로 사용할 수 있습니다.
주제와 관련된 이미지 근의 공식 만든 사람

근의 공식 만든 사람 주제와 관련된 이미지 48개를 찾았습니다.






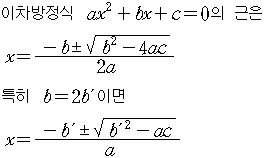


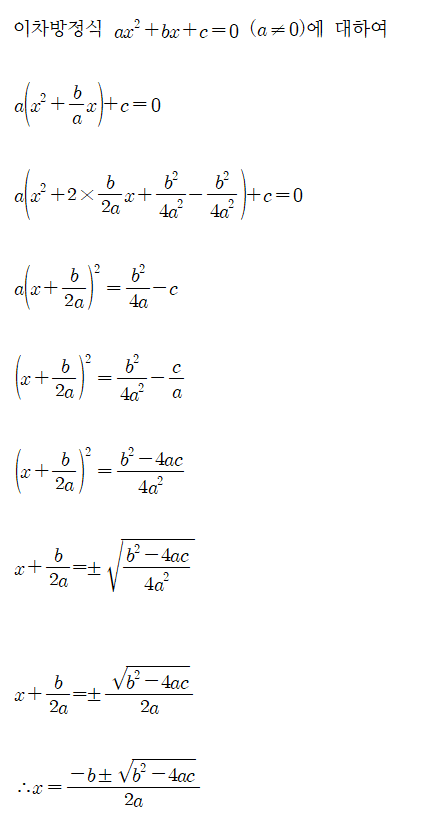



![문제적남자] 카이스트 레전드 졸업생의 풀이! 근의 공식 집착해서 망한 이장원 - YouTube 문제적남자] 카이스트 레전드 졸업생의 풀이! 근의 공식 집착해서 망한 이장원 - Youtube](https://i.ytimg.com/vi/2CinIGXmHUk/maxresdefault.jpg)
Article link: 근의 공식 만든 사람.
주제에 대해 자세히 알아보기 근의 공식 만든 사람.
- 확 풀어 준다! 근의 공식과 평양냉면 – 동아사이언스
- 근의 공식의 역사 : 네이버 블로그
- 근의 공식의 역사 by 주은 이 – Prezi
- 이차방정식의 역사
- 고차방정식 해법의 역사 – 과학의 지평 – KIAS
- 알콰리즈미 – 나무위키
더보기: b1.brokengroundgame.com/krblog

