근의 공식 유도
이차 방정식은 변수 x를 제곱한 항이 있는 방정식을 말한다. 이를 일반적으로 ax^2 + bx + c = 0의 형태로 나타낼 수 있다. 여기서 a,b,c는 상수이며, a가 0이 아니어야 한다.
이차 방정식의 근의 개념
이차 방정식에서 근은 방정식을 만족시키는 x값을 의미한다. 이차 방정식은 일반적으로 2개의 근을 가지며, 이는 복소수 근을 포함한다. 복소수 근은 실수 근과 복소수 근의 합으로 나타낼 수 있다.
이차 방정식의 근의 공식
이차 방정식의 근의 공식은 다음과 같다.
x = (-b ± √(b^2 – 4ac))/2a
여기서 ±는 더하기, 또는 빼기를 의미한다. 이 식은 알파벳 글자들로 이루어진 계수 a,b,c와 방정식의 근 x를 연결하는 식이며, 이차 방정식에서 유일한 근을 계산한다.
근의 공식의 유도 과정
디오판토스의 이론을 통해 이차 방정식의 근의 공식을 유도할 수 있다. 이는 다음과 같은 과정으로 이루어진다.
1. ax^2+bx+c=0과 같은 이차 방정식을 가정한다.
2. x에 대한 이차 항을 완전제곱식으로 나타내고, 상수항을 가져와 완전제곱식과 더해준다. 이로 인해 식이 다음과 같이 변한다.
ax^2+bx = -c
ax^2+bx+(b/2)^2 = (b/2)^2 -c
3. 양변에 (b/2)^2를 더하고 2a로 나눠준다.
ax^2+bx+(b/2)^2 = (b/2)^2 -c
(a/2x + b/2a)^2 = (b^2 – 4ac)/4a^2
4. 각 변에 루트를 씌워주면 최종적으로 근의 공식이 도출된다.
(a/2x + b/2a) = ± √(b^2 – 4ac)/2a
ax = -b ± √(b^2 – 4ac)/2a
근의 공식의 활용
근의 공식은 이차 방정식에서 근을 구하기 위해 필요한 공식이다. 이를 통해, 이차 방정식의 근을 계산할 수 있다.
예를 들어, 이차 방정식인 2x^2 + 5x – 3 = 0의 근을 구하기 위해 근의 공식을 이용하면 다음과 같다.
x = (-5 ± √(5^2 – 4(2)(-3))) / 2(2)
x = (-5 ± √49) / 4
x = (-5 ± 7)/4
따라서, 이차 방정식 2x^2 + 5x – 3 = 0의 근은 -3/2 또는 1/2이다.
근의 공식의 한계와 대안
근의 공식은 이차 방정식에서 유용하게 사용되지만, 일부 한계점이 있다. 이에 대한 대안도 고려해봐야 한다.
1. 근의 공식 쓰는 이유
근의 공식은 이차 방정식에서 근을 구하는데 있어 필수적인 공식이다. 이는 이차 방정식을 푸는 데에 있어 다양한 방법 중 하나이며, 이를 알아두는 것은 수학을 공부하는 데 도움이 된다.
2. 홀수 근의 공식
이차 방정식은 일반적으로 2개의 근을 가지는데, 한 개의 근만 필요한 경우는 홀수 근의 공식을 사용할 수 있다. 하지만, 이 경우에는 근의 공식보다 다른 방법이 더 간단하다.
3. 근의 공식 만든 사람
근의 공식은 16세기 이탈리아 수학자 디오판토스에 의해 유도되었다.
4. 삼차방정식 근의공식
삼차 방정식에서는 근의 공식을 사용할 수 없으며, 대신에 카르다노의 공식이나 네이퍼의 로그러리즘 등의 방법을 사용해야 한다.
5. 근의 공식 영어로
근의 공식은 ‘Quadratic Formula’로 알려져있다.
6. 근의 공식 정의
근의 공식은 이차 방정식에서 근을 구하기 위한 공식이다.
7. 근과 계수의 관계
이차 방정식의 근은 방정식의 계수와 직접적인 관계가 있다. 이는 근의 공식에서도 나타난다.
8. 근의 공식 활용
이차 방정식은 다양한 분야에서 활용되며, 근의 공식도 그 중 하나이다. 이를 통해, 이차 방정식의 근을 구하는 데에 있어서 높은 정확도와 효율성을 보장한다.
FAQs
Q: 근의 공식을 사용하는 이유는 무엇인가요?
A: 근의 공식은 이차 방정식에서 근을 구하는 데에 필요한 공식입니다. 이를 알아두는 것은 수학을 공부하는 데에 도움이 됩니다.
Q: 홀수 근의 공식이 뭔가요?
A: 홀수 근의 공식은 근이 한 개일 때 사용하는 공식입니다. 하지만, 이 경우에는 근의 공식보다 다른 방법이 더 간단합니다.
Q: 근의 공식을 만든 사람은 누구인가요?
A: 근의 공식은 16세기 이탈리아 수학자 디오판토스에 의해 유도되었습니다.
Q: 이차 방정식 외에도 근의 공식을 사용할 수 있나요?
A: 근의 공식은 이차 방정식에서만 사용할 수 있습니다.
Q: 근의 공식의 정의는 무엇인가요?
A: 근의 공식은 이차 방정식에서 근을 구하기 위한 공식입니다.
Q: 근의 공식은 어떤 수학 분야에서 사용되나요?
A: 근의 공식은 이차 방정식을 해결하는 데에 필요한 공식입니다. 이차 방정식은 수학뿐만 아니라 공학, 물리학, 경제학 등 다양한 분야에서 사용됩니다.
Q: 근의 공식을 적용할 때, 근과 계수는 어떤 관계가 있나요?
A: 이차 방정식의 근은 방정식의 계수와 직접적인 관계가 있습니다. 이는 근의 공식에서도 나타납니다.
Q: 근의 공식을 사용할 때, 어떤 한계점이 있나요?
A: 근의 공식은 이차 방정식에서 유용하게 사용될 수 있지만, 삼차 방정식 등에서는 근의 공식을 사용할 수 없습니다. 이에 대한 대안이 필요합니다.
Q: 근의 공식을 사용하는 것 이외에도 이차 방정식의 근을 구할 수 있는 방법이 있나요?
A: 이차 방정식을 푸는 방법 중에는 근의 공식 이외의 다양한 방법이 존재합니다. 대표적인 방법으로는 완전제곱식 방법, 피타고라스 정리 방법 등이 있습니다.
사용자가 검색한 키워드: 근의 공식 유도 근의 공식 쓰는 이유, 홀수 근의 공식, 근의 공식 만든 사람, 삼차방정식 근의공식, 근의 공식 영어로, 근의 공식 정의, 근과 계수의 관계, 근의 공식 활용
Categories: Top 48 근의 공식 유도
[EBS 수학의 답] 이차방정식 – 13. 근의 공식의 유도 과정
여기에서 자세히 보기: b1.brokengroundgame.com
근의 공식 쓰는 이유
근의 공식은 수학에서 미분 불가능한 함수의 근을 구하는 방법 중 하나이다. 근의 공식을 이용하면 삼각함수, 지수함수, 로그함수 등의 근을 구할 수 있다. 이번 글에서는 근의 공식을 사용하는 이유를 알아보려고 한다.
근의 공식의 필요성
수학은 현실 세계를 모델링하기 위해 사용된다. 이 모델에서는 변수들이 다양한 값이 될 수 있다. 예를 들어, 강의 시간은 누가 강의하는지, 강의 내용은 어떤 내용인지, 동일한 강의라 하더라도 수강생들의 능력 수준에 따라 이해할 수 있는 정도가 다를 수 있다. 따라서, 수학적 모델에서 다양한 값이 나타날 수 있기 때문에 근을 구하는 것은 매우 중요하다.
어떤 함수의 근을 구하는 것은 일반적으로 미분으로 이루어진다. 그러나, 미분이 불가능한 함수는 근을 구하기가 어렵다. 이 경우 근의 공식을 사용하면 근을 구할 수 있다. 예를 들어, $x^2+1=0$와 같은 방정식의 근을 구하기 위해서는 $x=\pm\sqrt{-1}$이다. 본래 정의에서, 루트 안에는 음수가 들어갈 수 없다. 그러나, 복소수의 개념을 도입하면 이러한 식에서 근을 구할 수 있다.
결국, 근의 공식은 수학에서 미분 불가능한 함수의 근을 구할 수 있는 유일한 방법 중 하나이다. 이유를 좀 더 자세히 살펴보자.
그렇다면, 근의 공식은 어떻게 동작하는가?
근의 공식은 일반적으로 다음과 같이 표현된다.
$a x^2 + b x + c = 0$
$x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$
여기서 $a, b, c$는 실수이며, $a$는 0이 아니다.
이 식에서 근의 공식을 통해 변수 $x$를 구할 수 있다. 그리고, 그 값을 대입한 식이 원래의 식과 동일하게 된다. 따라서, 근의 공식은 단순히 방정식의 근을 구하는 방법이다.
또한, 근의 공식은 이차방정식이 아닌 경우에도 적용이 가능하다. 예를 들어, $x^3+2x^2-x-1=0$ 식의 근을 구하는 경우, 먼저 $x=1$이라는 간단한 근을 찾는다. 그러면, $x=1$을 대입한 후 나머지 부분을 이차방정식의 형태로 나타낼 수 있다. 이렇게 하면 $x=1$, $x=-1+\sqrt{2}$, $x=-1-\sqrt{2}$의 세 개의 근을 찾을 수 있다. 즉, 근의 공식은 이차방정식에서 뿐만 아니라, 고차 방정식에서도 적용할 수 있는 능력이 있다.
근의 공식의 유용성
근의 공식은 매우 유용하다. 예를 들어, $sin(x)=0$의 근을 찾아보자. 이 식에서 $sin(x)=0$이 되는 x의 값은 $\pi$의 정수배이다. 그러나, 이러한 방정식을 모두 구할 수 있다는 보장은 없다. 이 경우, 근의 공식을 사용하면 수학적으로 정확한 값을 찾을 수 있다.
또한, 근의 공식은 적분이나 미분과 같은 다른 수학적 개념과도 밀접하게 관련이 있다. 이러한 관계는 미적분학에서 근의 공식이 중요한 개념이라는 것을 나타낸다. 예를 들어, 함수 $f(x)$가 주어졌을 때, $f(x)$의 근을 찾는 것은 $f’(x)$의 영점을 찾는 것과 같다. 이렇게 하는 것은 원래 문제에서 유용한 값을 찾는 것과 같다.
FAQs
Q: 근의 공식을 사용하는 이유가 무엇인가요?
A: 근의 공식은 미분 불가능한 함수의 근을 구하는 유일한 방법 중 하나입니다.
Q: 근의 공식은 어떤 경우에 유용한가요?
A: 근의 공식은 삼각함수, 지수함수, 로그함수 등의 근을 구할 때 유용합니다.
Q: 근의 공식은 고차 방정식에서도 적용할 수 있는가요?
A: 예, 근의 공식은 이차방정식에서 뿐만 아니라, 고차 방정식에서도 적용할 수 있습니다.
Q: 근의 공식과 적분, 미분은 어떤 관계가 있나요?
A: 근의 공식은 적분이나 미분과 같은 다른 수학적 개념과도 밀접하게 관련이 있습니다. 이 관계는 미적분학에서 근의 공식이 중요한 개념이라는 것을 나타냅니다.
Q: 근의 공식을 사용하지 않고 근을 구하는 방법은 있나요?
A: 그렇습니다. 삼분법, 뉴튼법, 단순한 근을 나누는 방법 등의 다양한 방법이 있습니다. 그러나, 근의 공식을 사용하면 정확한 값을 쉽게 찾을 수 있습니다.
Q: 근의 공식을 배울 때 가장 중요한 것은 무엇인가요?
A: 근의 공식을 이용해 문제를 해결할 수 있는 능력을 기르는 것이 가장 중요합니다. 또한, 근의 공식이 언제 사용될 수 있는지를 이해하는 것도 중요합니다.
홀수 근의 공식
What is the odd root formula?
The odd root formula is a mathematical formula that helps solve equations with odd roots. If a polynomial equation has an odd root, then the odd root formula can be used to find the value of that root.
The odd root formula is as follows:
If f(x) = ax^n + bx^(n-1) + … + mx^2 + nx + p, where n is odd, and a ≠ 0, then the equation f(x) = 0 has at least one real root.
This formula states that any odd degree polynomial equation has at least one real root. The formula can be derived by considering the behavior of polynomial functions as they approach positive and negative infinity.
Why is the odd root formula important?
The odd root formula is essential in solving polynomial equations. Polynomial equations are common in many areas of mathematics, including calculus, algebra, and geometry. The odd root formula allows mathematicians to find solutions to polynomial equations with odd roots, which would otherwise be difficult to solve.
The odd root formula is also useful in graphing polynomial functions. Knowing that a polynomial function has at least one real root means that the graph of that function must cross the x-axis at least once. This information can help mathematicians sketch the graph of a polynomial function.
How to use the odd root formula
To use the odd root formula to solve a polynomial equation, follow these steps:
Step 1: Identify the polynomial equation to be solved.
Step 2: Check if the degree of the polynomial equation is odd. If the degree is even, the odd root formula cannot be used.
Step 3: Check if the leading coefficient is not equal to zero. If the leading coefficient is equal to zero, the odd root formula cannot be used.
Step 4: Use the odd root formula to solve for the real root(s) of the equation.
Step 5: Check the answer by substituting the value(s) obtained in step 4 back into the original equation. The result should equal zero.
Let’s take an example:
Find the roots of the equation f(x) = 2x^3 – 3x^2 + 4x – 5
Step 1: Identify the polynomial equation to be solved.
The polynomial equation is f(x) = 2x^3 – 3x^2 + 4x – 5
Step 2: Check if the degree of the polynomial is odd.
The degree of the polynomial is odd (n = 3)
Step 3: Check if the leading coefficient is not equal to zero.
The leading coefficient (a) is equal to 2, which is not equal to zero.
Step 4: Use the odd root formula to solve for the real root(s) of the equation.
Since the degree of the polynomial is odd and the leading coefficient is not equal to zero, we can apply the odd root formula.
The formula states that if f(x) = 0, then there is at least one real root.
We can use the formula to find an approximate value for the root by trial and error.
Let’s try substituting x = 1 into the equation:
f(1) = 2(1)^3 – 3(1)^2 + 4(1) – 5
f(1) = -2
Let’s try substituting x = 2 into the equation:
f(2) = 2(2)^3 – 3(2)^2 + 4(2) – 5
f(2) = 11
Since the sign of the function changes from negative to positive between x = 1 and x = 2, we know that there must be a root between these values.
We can continue to use the odd root formula to find a more accurate value for the root. One way to do this is to use a process called Newton’s method. This involves finding the tangent line to the graph of the equation at the point where x = 1 (or the point where the function is negative), and finding where that line intersects the x-axis. That point is then used to find a new tangent line, and the process is repeated until an accurate value for the root is obtained.
By using this process, we can find that the root of the equation f(x) = 2x^3 – 3x^2 + 4x – 5 is approximately x = 1.8605
Step 5: Check the answer by substituting the value(s) obtained in step 4 back into the original equation. The result should equal zero.
f(1.8605) = 2(1.8605)^3 – 3(1.8605)^2 + 4(1.8605) – 5
f(1.8605) ≈ 0
Therefore, x = 1.8605 is a root of the equation f(x) = 2x^3 – 3x^2 + 4x – 5.
FAQs
Q. Can the odd root formula be used to solve polynomial equations with even roots?
A. No. The odd root formula is only applicable to polynomial equations with odd roots.
Q. Can the odd root formula be used to find complex roots?
A. No. The odd root formula only finds real roots. Complex roots can be found using other methods, such as the quadratic formula.
Q. Can the odd root formula be used to find all roots of a polynomial equation?
A. No. The odd root formula only guarantees the existence of at least one real root. Other roots may exist, but they may be complex or irrational.
Q. Is there a similar formula for even root equations?
A. Yes, there is a formula for even root equations called the even root formula. The even root formula states that if f(x) = 0, then there is at least one real root if and only if the leading coefficient is positive and the degree of the polynomial is even.
In conclusion, the odd root formula is an important tool in solving polynomial equations with odd roots. It guarantees the existence of at least one real root, which is helpful in graphing polynomial functions and finding solutions to real-world problems. By following the steps outlined in this article, mathematicians can use the odd root formula to find accurate values for the roots of polynomial equations with odd degrees.
주제와 관련된 이미지 근의 공식 유도
![[EBS 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정 [EBS 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정](https://b1.brokengroundgame.com/wp-content/uploads/2023/06/hqdefault-2040.jpg)
근의 공식 유도 주제와 관련된 이미지 43개를 찾았습니다.



![근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그 근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAxNzA3MThfMjgy/MDAxNTAwMzAzNjcwODM5.0Ko4eayHLraJjbWm_hrgK5JkmFTP7Ua85L_GU76sRncg.91v_26VXmz4pH4niVQckwPahti1BvTE2oqfwWng6pcIg.JPEG.pss2072/%EA%B7%BC%EC%9D%98%EA%B3%B5%EC%8B%9D_%EC%9C%A0%EB%8F%84.jpg?type=w420)
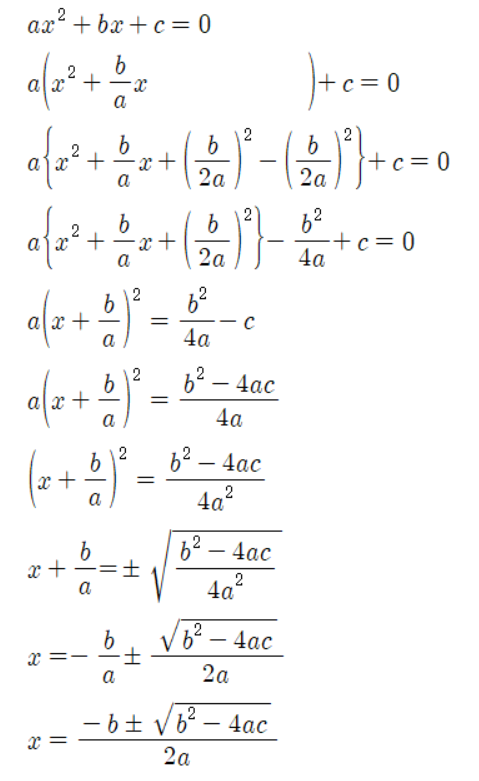






![이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기) 이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기)](https://blog.kakaocdn.net/dn/b16TIv/btqEljBSogl/AskNAzMjpxr8NvnoGImOlK/img.png)

![중3수학] 근의공식 유도과정 (이차방정식 근의공식) #shorts - YouTube 중3수학] 근의공식 유도과정 (이차방정식 근의공식) #Shorts - Youtube](https://i.ytimg.com/vi/356KWpjobAA/maxresdefault.jpg)

























Article link: 근의 공식 유도.
주제에 대해 자세히 알아보기 근의 공식 유도.
- 근의 공식, 근의 공식 유도, 짝수 공식 – 수학방
- [이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 …
- [이차방정식]근의 공식 및 유도하기 – 제이의 집
- 근의 공식 증명 복습 – 칸아카데미
더보기: b1.brokengroundgame.com/krblog

