근의공식
1. 근의공식이란 무엇일까?
근의공식은 일반적인 형태로 ax^2 + bx + c = 0 (단, a ≠ 0) 으로 표현된 이차방정식을 해결하는 수식으로, 다음과 같다.
x = (-b ± √(b^2 – 4ac)) / 2a
여기서, √ 는 루트를 나타내며, 즉 많이 사용하는 두 가지 공식은 다음과 같다.
x1,2 = (-b ± √(b^2 – 4ac)) / 2a (일반형)
x1,2 = (-b ± √b^2 – 4ac) / 2a (간단형)
2. 근의공식의 역사와 기원은 어디에 있을까?
근의공식의 역사는 매우 오래 된 것으로, 이차방정식은 인도의 대수학자 Brahmagupta가 7세기에 처음으로 발견했다. 이후 중국의 Zhu Shijie와 Perisan의 Al-Khwarizmi, 그리고 이듬해에 이어진 이탈리아의 Cardano 등 많은 수학자들이 이 식을 발견하고 연구하였다. 이후 근의공식은 다양한 상황에서 적용될 수 있게되며 수많은 연구자들에 의해 발전되었으며 현재는 일반적인 대학의 수학 교육을 통해 많은 학생들에게 알려지게되어 있다.
3. 근의공식의 종류와 예시는 무엇이 있을까?
근의공식에는 일반적인 형태의 공식뿐만 아니라, 앞에 항이 없는 일차방정식과 같은 비교적 단순한 형태의 공식도 있다. 일반형 근의공식 외에도 짝수 근의 공식, 홀수 근의 공식 등 다양한 형태의 근의 공식이 있다.
– 짝수 근의 공식 유도근의공식
x^2 = a
x = ±√a
– 일반적인 형태의 근의 공식
ax^2 + bx + c = 0 (단, a ≠ 0)
x = (-b ± √(b^2 – 4ac)) / 2a (일반형)
x = (-b ± √b^2 – 4ac) / 2a (간단형)
– 라디칼 근의 공식
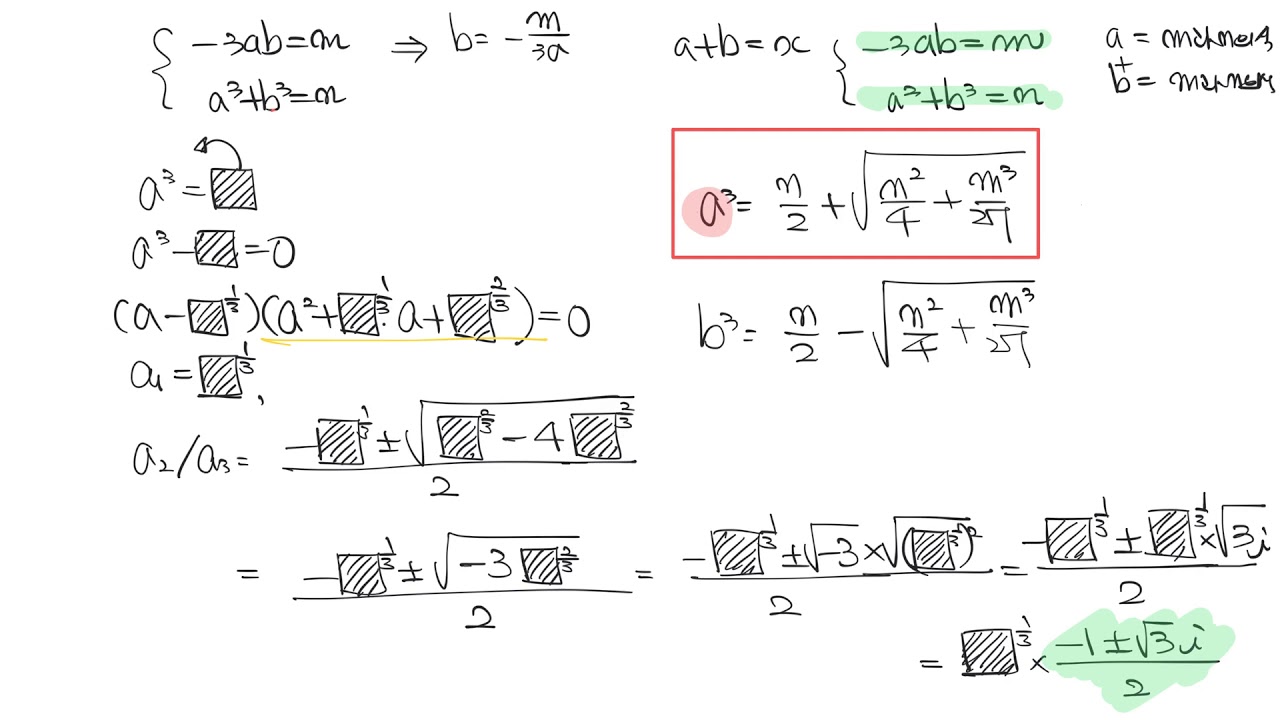
ax^3 + bx^2 + cx + d = 0 (단, a ≠ 0)
이 식을 해결하기 위해서는 고등학교 이상의 수준이 필요하며 복잡한 계산과 근 또는 부정 방정식의 해를 얻는 것이 중요하다.
– 이차방정식에서의 근의 공식
ax^2 + bx + c = 0 (단, a ≠ 0)
x = (-b ± √(b^2 – 4ac)) / 2a (일반형)
x = (-b ± √b^2 – 4ac) / 2a (간단형)
4. 근의공식을 이용한 해를 구하는 방법은 무엇일까?
이차방정식의 해를 구하는 방법은 다음과 같다.
1. 일반형이 아닌 경우, 예를 들어, 간단한 형태인 ax^2 + bx + c = 0일 때, 근의 공식은 다음과 같이 작성할 수 있다.
x = (-b ± √b^2 – 4ac) / 2a
2. 가장 적절한 공식을 선택하여 b^2-4ac 식의 갑을 계산한다.
3. x 값을 구하기 위해 ± 부호 뒤에 있는 부울리언 값이 +일 경우, x의 값을 구할 때에는 토글을 추가하지 않아도 된다.
4. 만약 부울리언 값이 – 인 경우, 토글 연산을 통해 값을 변경 후 식을 계산한다.
5. 근의 공식으로 부터 얻은 x 값을 원래의 이차 방정식에 대입하고 그 값이 맞는지 확인한다.
이와 같은 방법을 통해 이차방정식의 해를 빠르고 정확하게 구할 수 있다.
5. 근의공식과 관련된 응용 문제는 어떤 것이 있을까?
근의공식은 일상생활 전반적으로 유용하며 다양한 문제에 적용될 수 있다. 예를 들면, 일자 Algebra 문제, 미분 및 적분 문제 등에 이용이 가능하며, 엔지니어링 등의 분야에서도 이차방정식을 이용한 문제 해결 능력은 중요한 역할을 한다.
6. 수학적인 개념으로서의 근의공식과는 어떤 관계가 있을까?
수학적인 개념으로 근의 공식은 이차방정식의 마찬가지로 중요한 개념이다. 이를 통해 미분과 적분 등 다양한 수학적 개념에 대한 이해와 응용을 할 수 있다. 또한, 근의 공식은 현대 수학적 발전에서 중요한 역할을 하고 있으며, 다양한 분야에서의 문제해결 능력을 향상시키는데 큰 도움을 준다.
7. 근의공식의 활용과 유용성에 대해 생각해보자.
근의공식은 이차방정식을 해결하는 가장 기본적인 방법 중 하나이다. 이를 이용하여 모든 종류의 이차방정식의 해결을 가능하게하며, 미분과 적분 등 다양한 수학적 개념과도 밀접하게 연결된다. 이를 통해 다양한 상황에서 유용하게 사용할 수 있으며, 대학에서 수학과 공학, 자연과학 등 다양한 분야에서도 적극적으로 사용되고 있다.
FAQs
– 근의 공식은 무엇인가?
근의 공식은 이차방정식을 해결하는 수식으로, 함수가 x-axis와 만나는 지점을 찾는 방법 중 하나이다.
– 근의 공식을 이용하여 어떤 문제를 해결할 수 있는가?
근의 공식은 일상생활 전반적으로 적용이 가능하며, 일자 Algebra 문제, 미분 및 적분 등 다양한 문제를 해결할 수 있다.
– 짝수 근의 공식 유도근의공식이란 무엇인가?
짝수 근의 공식 유도근의 공식은 x^2 = a 과 같은 이차방정식을 해결하는 것이다. x = ±√a 로 간단하게 표현할 수 있다.
– 근의 공식은 어떤 방식으로 발견되었는가?
근의 공식은 7세기 인도에서 Brahmagupta가 처음 발견하였으며 이후 Zhu Shijie와 Al-Khwarizmi, Cardano 등 수많은 연구자들에 의해 발전되고 연구되었다.
– 근의 공식은 어떤 수학적 개념과 연결되어 있는가?
근의 공식은 재귀함수 겸 turing machine을 turing machine을 이용한 모델링을 예로 들 수 있다. 또한, 근의 공식은 미분과 적분 등 다양한 수학적 개념과도 밀접하게 연결되어 있다.
사용자가 검색한 키워드: 근의공식 짝수 근의 공식 유도
Categories: Top 24 근의공식
[EBS 수학의 답] 이차방정식 – 13. 근의 공식의 유도 과정
여기에서 자세히 보기: b1.brokengroundgame.com
짝수 근의 공식 유도
짝수 근의 공식은 2차 방정식에서 근이 짝수인 경우, 이를 구하는 공식을 말한다. 이 공식은 근의 공식 중 하나로, 이차 방정식의 근을 구하는 방법은 총 3가지가 있으며, 그 중 하나가 짝수 근의 공식이다.
짝수 근의 공식은 다음과 같다.
x = -b/2a ± √(b² – 4ac)/2a
여기서 a, b, c는 2차 방정식의 각각의 계수를 의미한다.
위의 공식에서 알 수 있듯이, 짝수 근의 공식은 이차 방정식의 계수와 루트 안에 있는 값에 따라 달라진다.
짝수 근의 공식 유도 과정은 어떤 것인가?
짝수 근의 공식 유도는 이차 방정식에서 x의 값을 구하는 방법 중 하나로, 아래와 같이 유도할 수 있다.
2차 방정식의 일반식은 아래와 같다.
ax² + bx + c = 0
여기서 a, b, c는 각각 상수이며 a ≠ 0이다.
이 때, x = 2m를 대입하면,
a(2m)² + b(2m) + c = 0
4am² + 2bm + c = 0
여기서 2를 나눈 다음,
2am² + bm + c/2 = 0
이를 x = -b/2a로 나누면,
x² + (c/2a) = -b/2a x
위의 식을 제곱하면,
x⁴ + 2(c/2a) x² + (c/2a)² = (b/2a)² x²
x⁴ + (c/a) x² + (c/2a)² – (b/2a)² x² = 0
여기서,
(m)⁴ + (c/a) (m)² + (c/2a)² – (b/2a)² = 0
이렇게 함으로서, 짝수 근의 공식을 얻을 수 있다.
그러나, 이러한 유도 과정은 매우 복잡하며, 쉽게 이해하기 어려울 수 있다. 따라서, 일반적으로 학생들은 유도보다는 짝수 근의 공식을 적용하여 문제를 푸는 것이 더욱 편리하다.
짝수 근의 공식의 사용 예제는 무엇인가?
2차 방정식에서 짝수 근의 공식은 아래와 같이 적용된다.
예를 들어, 다음과 같은 2차 방정식을 생각해보자.
2x² + 6x + 3 = 0
이 경우, 위에서 소개한 공식을 사용하여 짝수 근의 값을 찾을 수 있다.
먼저, 각각의 계수를 식에 대입한다.
x = -b/2a ± √(b² – 4ac)/2a
= -6/4 ± √(6² – 4(2)(3))/4
= -3/2 ± √(6 – 3)/2
= -3/2 ± (1/2)√3
따라서, 이차 방정식의 근은 -3/2 ± (1/2)√3의 두 값을 가진다.
짝수 근의 공식을 사용하여 이차 방정식을 해결하는 것은 매우 쉬우며, 실용적인 측면에서 유용하다.
FAQs
Q: 짝수 근의 공식이란 무엇인가?
A: 2차 방정식에서 근이 짝수인 경우, 이를 구하는 공식을 말한다.
Q: 짝수 근의 공식 유도 과정은 어떤 것인가?
A: 유도 과정은 매우 복잡하지만, 일반적으로 짝수 근의 공식을 적용하여 문제를 해결하는 것이 더욱 편리하다.
Q: 짝수 근의 공식의 응용 예제는 무엇인가?
A: 예를 들어, 2x² + 6x + 3 = 0과 같은 2차 방정식을 푸는 경우 짝수 근의 공식을 적용할 수 있다.
Q: 짝수 근의 공식이 유용한 이유는 무엇인가?
A: 짝수 근의 공식을 사용하여 2차 방정식의 근을 구하는 것은 매우 쉽고 효과적이다. 이를 통해 실제 문제에서 빠르고 쉽게 근을 구할 수 있다.
Q: 짝수 근의 공식 외에도 2차 방정식의 근을 구하는 방법은 무엇이 있는가?
A: 2차 방정식의 근을 구하는 방법은 총 3가지가 있으며, 짝수 근의 공식 외에도 공식을 이용하는 방법과 완전제곱수를 이용하는 방법이 있다.
Q: 2차 방정식이 어떤 응용 분야에서 사용되는가?
A: 2차 방정식은 수학뿐만 아니라 공학분야에서도 많이 사용되며, 예를 들어, 물체가 떨어지는 시간이나 거리, 속도 등을 구하는 데 사용된다.
Q: 짝수 근의 공식은 언제 사용되는가?
A: 짝수 근의 공식은 근이 짝수인 경우 2차 방정식의 근을 구하는 데 사용된다.
Q: 2차 방정식에서 근이 0인 경우, 어떻게 해결할 수 있는가?
A: 이 경우, 2차 방정식을 인수분해하여 (x-근)(x-근) 형태로 표현할 수 있다. 이를 통해 근이 0인 경우를 해결할 수 있다.
Q: 짝수 근의 공식을 사용하여 구한 값이 근이 아닌 거짓근인 경우, 어떻게 해결할 수 있는가?
A: 이 경우, 부정방정식의 근들을 다시 2차 방정식에 대입하여 실제 근을 구할 수 있다.
Q: 2차 방정식에서 근이 무리수 값인 경우, 어떻게 확인할 수 있는가?
A: 이 경우, 계수끼리의 비율이 유리수가 아닌 경우 근이 무리수인 것으로 확인할 수 있다.
주제와 관련된 이미지 근의공식
![[EBS 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정 [EBS 수학의 답] 이차방정식 - 13. 근의 공식의 유도 과정](https://b1.brokengroundgame.com/wp-content/uploads/2023/06/hqdefault-2053.jpg)
근의공식 주제와 관련된 이미지 10개를 찾았습니다.


![이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기) 이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기)](https://blog.kakaocdn.net/dn/CFxKW/btqEljhxYt2/Kq0oLoyjzCIIYbRDFKkGYk/img.png)


![주말N수학]'아듀~근의 공식' 2차 방정식 쉽게 푸는 새 방법 : 동아사이언스 주말N수학]'아듀~근의 공식' 2차 방정식 쉽게 푸는 새 방법 : 동아사이언스](https://image.dongascience.com/Photo/2020/01/3e487f319f747b7ff291cb1d0bf99f4a.jpg)





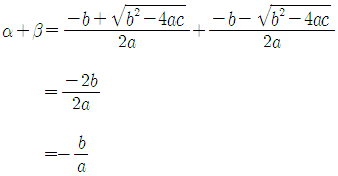









![근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그 근의공식/이차방정식의 풀이] 근의공식유도하기 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAxNzA3MThfMjgy/MDAxNTAwMzAzNjcwODM5.0Ko4eayHLraJjbWm_hrgK5JkmFTP7Ua85L_GU76sRncg.91v_26VXmz4pH4niVQckwPahti1BvTE2oqfwWng6pcIg.JPEG.pss2072/%EA%B7%BC%EC%9D%98%EA%B3%B5%EC%8B%9D_%EC%9C%A0%EB%8F%84.jpg?type=w420)












![프로그래머스] 레벨 2 : 카펫 - 카미유 테크 블로그 프로그래머스] 레벨 2 : 카펫 - 카미유 테크 블로그](https://user-images.githubusercontent.com/39554623/123511672-a75d3a80-d6bd-11eb-9968-1bd1a87322b9.png)



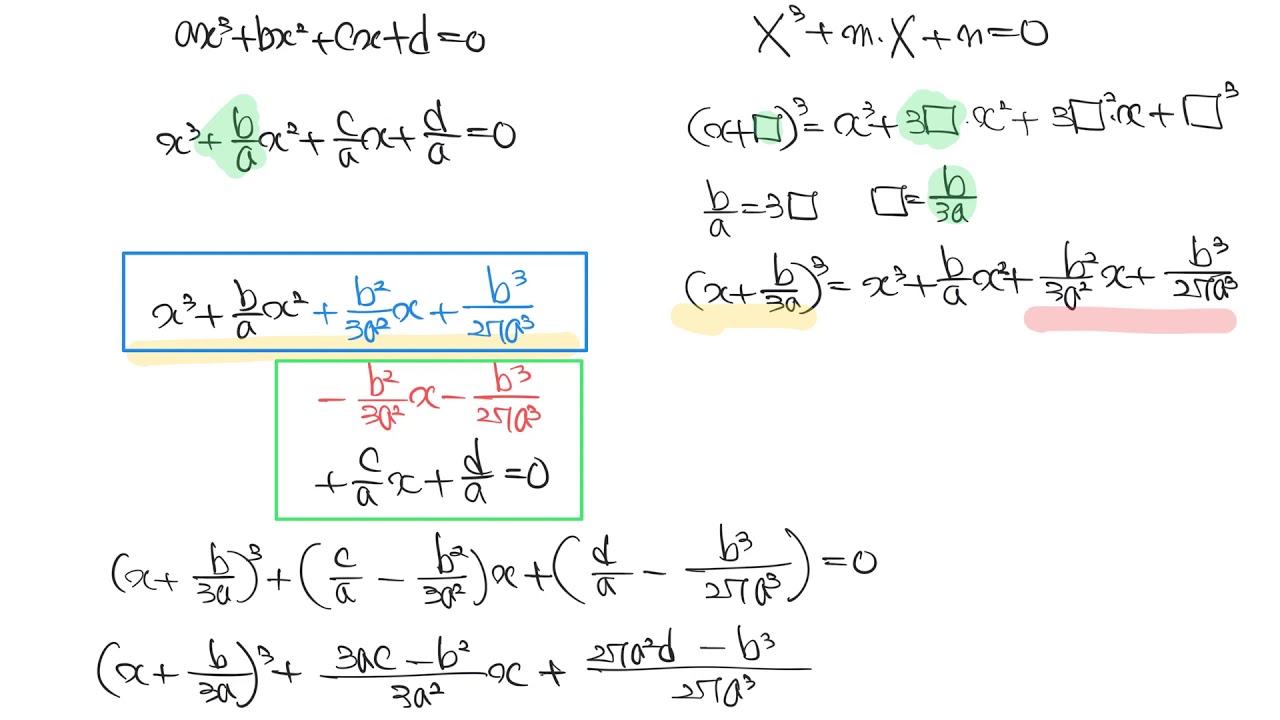
![모듈식 수학 (상)] 2. 방정식과 부등식 (13) 이차방정식의 풀이(근의공식) 모듈식 수학 (상)] 2. 방정식과 부등식 (13) 이차방정식의 풀이(근의공식)](https://t1.daumcdn.net/cfile/tistory/99E07E365BBC06C607)





Article link: 근의공식.
주제에 대해 자세히 알아보기 근의공식.
- 근의 공식을 몰라도 풀 수 있는 이차방정식 – 수학방
- 근의공식/이차방정식의 풀이 – 네이버 블로그
- 이차방정식의 근의 공식 이해하기 – 칸아카데미
- [이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 …
- [주말N수학]’아듀~근의 공식’ 2차 방정식 쉽게 푸는 새 방법
- 짝수 근의 공식 (이차방정식 짝수 공식) – 모든 수학
- 이차방정식의 근 구하는 법 (이미지 포함) – wikiHow
- 근 (수학) – 위키백과, 우리 모두의 백과사전
더보기: b1.brokengroundgame.com/krblog

