근의공식 짝수
근의공식 짝수는 짝수 차수의 다항식의 근을 구하는 공식이다. 여기서 차수란 다항식에서 가장 높은 차수를 뜻한다. 즉, 2차 이하의 다항식에서 근의공식 짝수를 적용할 수 있는데, 이러한 이유에서 근의공식 짝수는 이차방정식의 해를 구하는 데에 많이 사용된다.
근의공식 짝수의 정의와 개념
근의공식 짝수는 짝수 차수의 다항식의 근을 구하는 공식으로, x^n + a_{n-1}*x^(n-1) + … + a_1*x + a_0 = 0과 같은 짝수 차수의 다항식에서 근을 구할 수 있다. 이 공식은 일반적인 형태인 -b ± √(b^2 – 4ac) / 2a 에서 만들어진 것으로 실수값을 반환한다.
근의공식 짝수 증명 및 유도 방법
근의공식 짝수는 다음과 같이 증명할 수 있다.
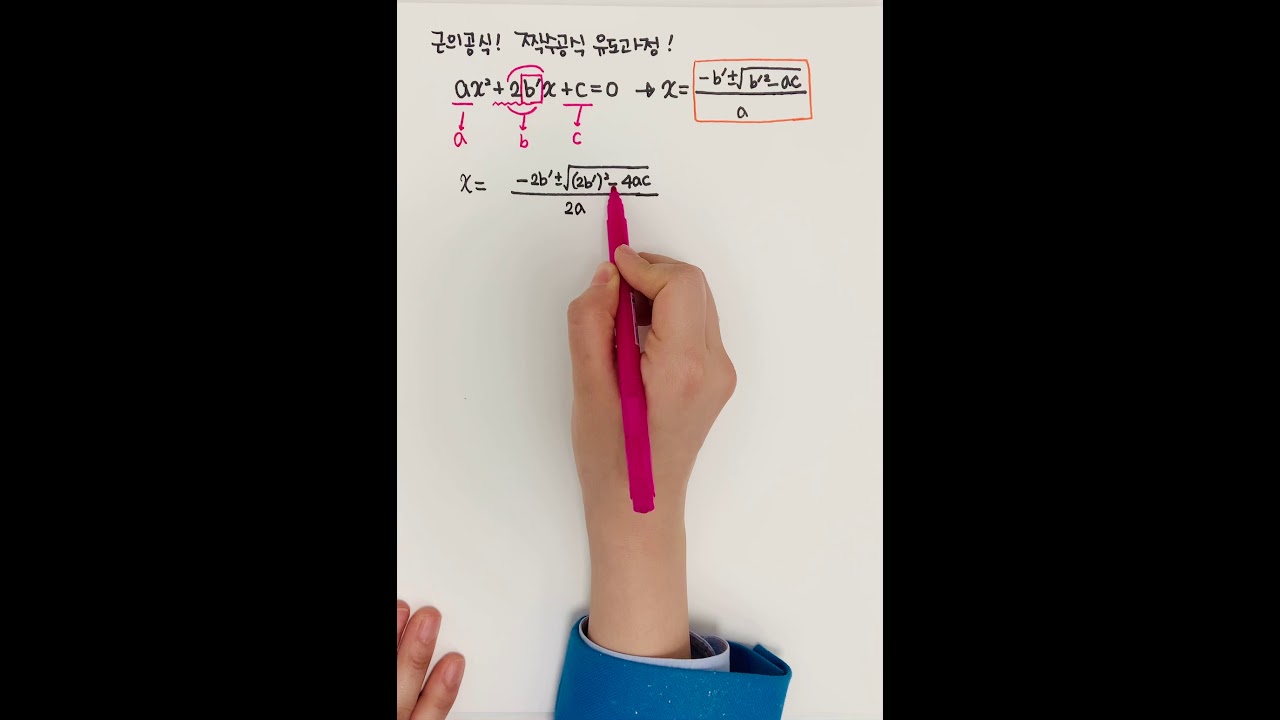
우선 2차 방정식의 근을 구하는 공식인 -b ± √(b^2-4ac) / 2a 에서 공식의 b와 c를 2n과 n^2로 치환해보자.
ax^2 + bx + c = 0
ax^2 + 2nx + n^2 – n^2 + bx + c = 0
a(x + n)^2 = n^2 – bx – c
(x + n)^2 = (n^2 – bx – c) / a
x + n = ±√((n^2 – bx – c) / a)
x = -n ± √((n^2 – bx – c) / a)
따라서, 증명결과 근의공식 짝수는 다음과 같다.
x = -n ± √((n^2 – bx – c) / a)
근의공식 짝수를 이용한 다항식 근의 구하기
1. 2차 이하의 다항식에서 근의공식 짝수를 이용할 수 있다.
2. 다음과 같이 a, b, c, d와 같은 다항식의 계수를 대입하고 계산을 하면 근을 구할 수 있다.
ax^4 + bx^3 + cx^2 + dx + e = 0 일 때,
x = -b / (4a) ± √((b^2-4ac) / (8a^2)) – 2c / (4a)
근의공식 짝수의 예시와 응용
예시 1.
x^4 + 3x^3 – 2x^2 + 7x – 6 = 0 의 해를 구해보자.
이 다항식은 4차 다항식이므로 근의공식 짝수를 적용할 수 있다.
a = 1, b = 3, c = -2, d = 7, e = -6 이므로,
x = -3 / 4 ± √(105 / 8) – 2 / 4
이다. 이는 대략 -2.1741과 0.6741으로 구할 수 있다.
예시 2.
x^6 + 4x^5 – 8x^4 – 22x^3 + 19x^2 + 40x – 24 = 0 의 해를 구해보자.
이 다항식은 6차 다항식이므로 근의공식 짝수를 적용할 수 있다. 하지만 이 경우 6차 다항식을 해결하기는 어렵다. 따라서 보통 분할정복법과 같은 다른 방법을 사용하거나 컴퓨터적인 방법을 사용하는 것이 일반적이다.
근의공식 짝수와 이차방정식 해의 구하기
이차방정식은 일반적으로 다음과 같은 형태를 가진다.
ax^2 + bx + c = 0
이 문제를 풀기 위해서는 근의공식 짝수를 이용할 수 있다. 따라서 이 식에 대입하면,
x = -b ± √(b^2 – 4ac) / 2a
이 된다. 이 공식을 이용해 이차방정식을 풀면 다음과 같은 예시가 나온다.
예시.
x^2 + 4x + 3 = 0 의 해를 구해보자.
a = 1, b = 4, c = 3 이므로,
x = -4 ± √(4^2 – 4 * 1 * 3) / 2 * 1
x = -4 ± 2
값으로 이루어진 두 해, -2와 -1이 나온다.
근의공식 짝수와 허수근 개념 이해하기
단항식의 크기는 실수 범위내에서 정의되지만, 중복근의 경우에는 유한한 (유리수) 해를 가지지 않는 경우가 있을 수 있다. 이런 경우에는 복소수 범위내의 허수가 사용되어 계산되며, 이를 허근이라고 하며 i라는 표기를 사용한다. 이 때 사용하는 것이 바로 근의공식 짝수이다.
따라서, 근의공식을 사용해 다항식의 해를 구할 경우에는, 이차항에서 만들어진 제곱근 값이 음수인 경우 허근이 생기며, 이는 다음과 같은 무한근과 같이 나타낼 수 있다.
√(-1) = i
√(4 * -1) = 2i
따라서, 근의공식 짝수를 사용할 때는 허근의 개념을 이해하고 있어야 한다.
근의공식 짝수와 실수근, 허수근 구분하기
여기에서는 근의공식 짝수를 이용해 실수근과 허수근을 구분하는 방법을 다루고자 한다.
짝수 차수의 다항식에서 근의공식 짝수를 적용해 계산을 진행할 경우, 실수 근을 구할 수 있는 경우는 제곱근 내에서 양수 값이 결과로 나옴을 알 수 있다. 반면, 내부 값이 음수가 나오는 경우에는, 허수 근을 구할 수 있다. 이때 내부 값이 음수인 경우의 결과값은 i가 포함될 수 있으며, 이를 허근이라 한다.
근의공식 짝수의 공식적 정의와 유용성 파악하기
근의공식 짝수는 다음과 같다.
x = -b ± √(b^2 – 4ac) / 2a
이 공식은 이차방정식의 해를 구하는 데에 많이 쓰이며, 복잡한 계산을 간편하게 해주는 유용한 공식이다. 근의공식을 사용하는 이유는, 매번 수식을 이용해 해를 도출하지 않고, 보다 쉽게 계산할 수 있기 때문이다.
여기에 이미 계산하려는 다항식의 차수가 짝수일 경우, 근의공식 짝수를 이용하기에 더욱 효율적인 결과를 제공할 수 있으며, 더 적은 시간과 노력으로 문제를 해결할 수 있다. 이를 통해 처음부터 많은 양의 시간과 노력을 차지하는 수식을 해결한다는, 근의공식의 유용성을 더욱 깊이 이해할 수 있다.
FAQs
1. 근의공식은 무엇인가?
– 근의공식은 다항식에서 해를 구하는 방법 중 하나이다.
2. 근의공식 짝수는 언제 사용되나요?
– 근의공식 짝수는 짝수 차수의 다항식에서 해를 구할 때 사용된다.
3. 근의공식을 어떻게 증명하나요?
– 근의공식 짝수의 유도는 이차방정식을 적용해 나온 결과다.
4. 근의공식을 이용한 다항식 근의 구하기가 어렵다면 어떻게 해야하나요?
– 분할정복법 등 다른 방법을 사용하거나 컴퓨터적인 방법을 사용하는 것이 일반적이다.
5. 근의공식을 사용할 때 허수근이란 무엇인가요?
– 근의공식을 사용할 때 제곱근 내부 값이 음수가 나오는 경우, 허수근이 생긴다.
6. 근의공식과 이차방정식은 어떻게 연관이 되나요?
– 근의공식은 이차방정식의 해를 구하는 데에 많이 사용된다.
7. 근의공식 짝수는 실수근과 허수근을 구분할 수 있나요?
– 근의공식을 사용할 때, 제곱근 내부 값이 양수인 경우 실수근이 나오며, 제곱근 내부 값이 음수인 경우에는 허수근이 나온다.
8. 근의공식이 언제 사용되나요?
– 근의공식은 다항식에서 해를 구하는 데에 많이 사용된다. 또한 짝수 차수의 다항식에서는 근의공식 짝수를 이용해 더욱 쉽게 문제를 해결할 수 있다.
사용자가 검색한 키워드: 근의공식 짝수 근의 공식 쓰는 이유, 홀수 근의 공식, 근의 공식 활용, 근의 공식 유도, 근의 공식 영어로, 근의 공식 계산기, 이차방정식 근의 공식, 근의 공식 만든 사람
Categories: Top 30 근의공식 짝수
중3-3-6. 짝수 근의 공식 (짝수 공식) feat. 증명, 유도
여기에서 자세히 보기: b1.brokengroundgame.com
근의 공식 쓰는 이유
근의 공식은 이차 방정식의 근을 구하는 방법 중 하나로, 일반적인 형태인 ax² + bx + c = 0의 방정식에서 x의 값을 구하는 방법이다. 이 차수 방정식은 두 개의 서로 다른 근을 가지거나, 중복된 근을 가질 수도 있다.
근의 공식은 일반적으로 다음과 같다:
x = (-b ± √b²-4ac) / 2a
여기서 a, b, c는 각각 방정식의 계수를 나타내며, √는 제곱근을 나타낸다. 이 공식은 이차 방정식의 두 개의 해를 찾는 데 사용된다.
근의 공식을 왜 사용하는가?
수학에서, 이차 방정식은 매우 중요한 개념이다. 이것은 원의 방정식이나, 곡선의 형태를 명확하게 분석할 때 사용된다는 점에서 매우 유용하다. 또한 물리학 및 공학에서도 자주 사용된다.
따라서, 이차 방정식의 근을 구하는 것은 매우 중요하다. 이것을 위해서 근의 공식을 사용한다. 근의 공식은 이차 방정식의 근을 찾는 가장 간단하고 효과적인 방법 중 하나이다.
또한, 근의 공식은 간단한 방법이지만, 대수학 수준은 매우 중요하다. 이것은 전문 수학자가 아니더라도 이해할 수 있기 때문에, 누구나 다룰 수 있는 중요한 수학 개념 중 하나이다.
근의 공식을 사용하여 이차 방정식의 근을 구하는 방법
이차 방정식의 근을 찾기 위해서는 다음과 같은 절차를 따르면 된다.
Step 1: 방정식의 계수 a, b, c를 알아낸다.
우선, 이차 방정식의 ax² + bx + c = 0에서 각각의 계수를 찾는다. 이것은 각 항에 있는 변수의 차수를 확인하고, 그와 관련된 계수를 찾는 것이다.
Step 2: 근의 공식을 사용하여 해를 분석한다.
앞서 언급한 방정식에서 근의 공식을 사용하여 x의 해를 찾을 수 있다. x = (-b ± √b²-4ac) / 2a을 사용하여 해를 구할 수 있다.
만약 근의 공식에서 √b² – 4ac가 음수이면, 이차 방정식은 실근을 가지지 않으며, 복소수 해를 가진다.
Step 3: 방정식의 근을 구한다.
근의 공식을 사용하여 x의 값을 구하면, 이것이 이차 방정식의 해가 된다. 만약 이차 방정식이 중복된 근을 가지고 있다면, 이것은 근의 공식을 사용하여 한 번만 계산하면 된다.
FAQs
1. 이차 방정식에서 근의 공식을 사용하는 것이 항상 가장 효과적인 방법인가요?
근의 공식은 이차 방정식의 해를 찾는 가장 간단한 방법 중 하나이다. 그러나 대부분의 경우, 이것은 근을 구하는 가장 효과적인 방법은 아니다. 예를 들어, 방정식이 인수분해 가능한 경우에는, 그 방법을 사용하는 것이 더 효과적이다.
2. 근의 공식은 모든 이차 방정식에서 사용 가능한가요?
근의 공식은 모든 이차 방정식에서 사용 가능하지만, 중복된 근을 가진 방정식의 경우, 근의 공식이 더욱 단순하게 만들어질 수 있다. 따라서, 중복된 근을 가진 이차 방정식에서는 다른 방법을 사용할 수도 있다.
3. 이차 방정식에서 방정식 해를 구하는 다른 방법이 있나요?
예, 이차 방정식의 해를 구하는 다양한 방법이 있다. 이 중 인수분해나, 완전 제곱 부분으로 나누어 계산하는 방법 등이 있다.
4. 근의 공식은 어디에 사용되나요?
근의 공식은 수학 분야뿐만 아니라, 물리학과 공학 등 자연과학 분야에서도 매우 중요하게 사용된다. 더 구체적으로는, 곡선 방정식의 형태를 명확히 분석하거나, 이차 방정식에 기반하여 이차 함수를 그리는 데 사용된다.
5. 근의 공식을 사용할 때 주의해야 할 점이 있나요?
긴 계산의 결과 x의 값이 유효한지, 계산하면서 실수할 가능성이 있는 부분을 미리 예측하며 풀어야 합니다. 따라서 근의 공식을 사용하여 해를 구할 때를 포함하여, 수학적인 계산을 수행하는 경우, 만약 해당 문제에 둘 이상의 풀이 방법이 있다면, 각각의 방법을 모두 고려해 볼 필요가 있다.
홀수 근의 공식
이 공식은 일반적인 이차방정식에서 해결하기 어려운 경우에 유용합니다. 예를 들어, 이차방정식 x² + 3x + 2 = 0의 해를 구하면 x = -1 또는 -2입니다. 이 지식은 이차방정식을 2개의 일차방정식으로 분해하여 해결하는 공식을 사용하여 구할 수 있습니다. 그러나, 이 공식은 이차방정식에 특별한 구조가 없는 경우에는 사용할 수 없습니다.
이것은 홀수 근의 공식이 중요한 이유 중 하나입니다. 이 공식은 모든 이차방정식에서 사용할 수 있으며, 특정한 구조를 가진 이차방정식을 해결할 수 있는 다른 방법과 함께 사용됩니다. 이 글에서는 홀수 근의 공식에 대해 자세히 살펴보겠습니다.
홀수 근의 공식의 유래
홀수 근의 공식은 중국 수학자 증정(曾丞)이 만든 공식입니다. 증정은 13세기 중국에서 활동하였으며 이차방정식을 해결하는 다른 방법을 개발한 중국의 유명한 수학자입니다.
증정은 홀수 근의 공식을 유도하는 방법을 발견했습니다. 이 방법은 이 차방정식을 완전제곱식의 차로 표현함으로써 이루어졌습니다. 그 결과, 이차방정식에서 홀수 근을 찾는 공식이 나타났습니다.
홀수 근의 공식 이용 방법
홀수 근의 공식을 사용하여 이차방정식 ax²+bx+c=0에서 홀수 근을 구하는 방법은 아래와 같습니다.
1. 방정식을 표준형으로 만듭니다. a≠0일 때, x²+(b/a)x+(c/a)=0으로 표현할 수 있습니다.
2. 이차항의 계수(a)에 따라 부호가 같은 변수 k를 정의합니다.(k=b/a or k=a/b)
3. 홀수 근을 찾기 위해 x = k − (b/2a)를 대입합니다.
4. 이 값을 이차방정식의 해로 확인합니다.
이 공식의 이해를 돕기 위해 실제 예시를 살펴봅시다. 이차방정식 x²+3x+2=0에서 홀수 근을 찾는 과정은 다음과 같습니다.
1. 이차방정식을 표준형으로 표현합니다. x²+3x+2=0은 (1)x²+(3)x+(2)=0으로 바꿀 수 있습니다.
2. 부호가 같은 변수 k를 정의합니다. 이 경우 k=3/1=3입니다.
3. x=k-(b/2a), 즉 x=3-(3/2*1)을 대입합니다. 이 값은 x=1입니다.
4. x=1을 이차방정식의 해로 대입합니다. (1)1²+3(1)+2=0이므로 이차방정식의 해는 x=1입니다.
이것은 이차방정식의 홀수 근을 구하는 공식의 작동 방식을 보여주는 예시입니다. 이 방식은 모든 이차방정식에 적용할 수 있으며, 다른 방법과 함께 사용됩니다.
홀수 근의 공식 FAQ
Q: 홀수 근의 공식을 사용할 때, 정수만을 구하고 싶을 때 어떻게 해야 할까요?
A: 이차방정식에서 홀수 근을 구할 때 생길 수 있는 문제 중 하나는 비정수적인 해를 얻는 것입니다. 이 경우, x의 부호와 b의 부호가 서로 같지 않아서 이차방정식의 해가 비정수가 됩니다.
정수 해만을 구하는 방법 중 하나는, 홀수 근의 공식에서 얻은 해가 정수이지 않으면, 이 차방정식의 다른 해도 정수가 아닌 홀수가 된다는 것을 이용하는 것입니다. 예를 들어, 이차방정식 x²+3x+2=0에서 홀수 근을 구할 경우 x=1과 x=-2의 두 가지 해가 있습니다. 홀수 근을 얻고 싶으면 x=1을 사용하면 됩니다.
Q: 이차방정식에서 해를 얻기 위해 다른 공식을 사용하는 방법이 있습니까?
A: 이차방정식은 일반적으로 매우 복잡하며, 해결하기 어렵습니다. 홀수 근의 공식은 이차방정식의 해를 구하는 간단한 방법 중 하나입니다. 그러나, 홀수 근의 공식을 사용할 수 없는 이차방정식도 있습니다. 이럴 경우, 더 복잡한 다른 공식을 사용해야 합니다. 이차방정식의 해결 방법은 수학의 깊이 있는 분야이며, 더 복잡한 공식을 하나하나 익히는 것이 필요합니다.
Q: 홀수 근의 공식이 두 근 모두 홀수인 경우가 있나요?
A: 이차방정식에서 두 근 모두 홀수인 경우는 없습니다. 이 이유는 홀수 근의 공식이 홀수 값을 정의해놓은 공식이기 때문입니다. 이 검증은 x의 부호와 b의 부호가 서로 같은 경우에도 성립합니다.
Q: 이차방정식의 근을 구하기 위해, 홀수 근의 공식 이외에 다른 방법이 있나요?
A: 이차방정식의 근을 구하는 방법은 홀수 근의 공식 이외에도 많이 있습니다. 이러한 방법 중 가장 일반적인 것은 일차방정식을 이용해 이차방정식을 분해하는 것입니다. 이 방법은 이차방정식을 완전제곱식의 차로 표현함으로써 새로운 방정식을 얻는 것입니다. 이 방식만큼이나 유용한 다른 방법으로는, 역치 방정식 이라는 방법도 있습니다. 이 방법은 완전제곱식의 차와 제곱항의 곱으로 이루어진 두 개의 식을 만들어 이차방정식과 결합합니다.
Q: 왜 홀수 근의 공식을 사용하는 경우가 더 많나요?
A: 홀수 근의 공식은 이차방정식의 근을 구하는 간단한 방법 중 하나입니다. 이 공식은 일반적인 이차방정식에서 해결하기 어려운 경우에 적합합니다. 또한, 해가 비정수인 경우에도 적용할 수 있습니다. 이 질문에 대한 대답은, 때로는 홀수 근의 공식과 다른 방법을 함께 사용해야하기 때문입니다. 이것은, 특정한 구조를 가진 이차방정식을 해결하기 위해서는 이러한 방법들을 모두 함께 사용해야만 한다는 것을 의미합니다.
근의 공식 활용
The Quadratic Formula or 근의 공식
The quadratic formula or 근의 공식 is used to find the roots of a quadratic equation. A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. The quadratic formula is given by:
x = [-b ± √(b^2 – 4ac)] / 2a
The quadratic formula can be derived by completing the square on the quadratic equation. It is a general formula that works for all quadratic equations, whether the roots are real or complex. If the discriminant, b^2-4ac, is negative, then the roots will be complex conjugates.
Application of Quadratic Formula in Korean
The quadratic formula or 근의 공식 is a fundamental tool in mathematics and can be used in many applications in Korean, such as physics, engineering, economics, and finance.
Physics
The quadratic formula is often used in physics to solve problems related to motion and gravity. For example, if an object is thrown upward with an initial velocity of v0, then its height h at time t can be calculated using the equation h = v0t – 1/2gt^2, where g is the acceleration due to gravity. To find when the object reaches its maximum height, we need to find the roots of the equation -1/2gt^2 + v0t + h = 0 using the quadratic formula.
Engineering
The quadratic formula is also used in engineering to calculate the maximum or minimum values of a function. This is useful, for example, in optimizing the performance of a machine or designing a bridge.
Economics
In economics, the quadratic formula is used in cost-benefit analysis to calculate the breakeven point. The breakeven point is the level of sales at which the revenue equals the total cost. To find the breakeven point, we need to solve the equation R(x) = C(x), where R(x) is the revenue function and C(x) is the cost function. This equation can be quadratic in nature and solved using the quadratic formula.
Finance
In finance, the quadratic formula is used to calculate the yield to maturity of a bond. The yield to maturity is the return an investor will receive if they hold a bond until it matures. It is calculated by solving the quadratic equation P = C/(1+r)^1 + C/(1+r)^2 + … + C/(1+r)^n + F/(1+r)^n, where P is the price of the bond, C is the coupon payment, r is the yield to maturity, F is the face value, and n is the number of years until maturity.
FAQs
1. What is the quadratic formula or 근의 공식?
The quadratic formula or 근의 공식 is a mathematical formula used to find the roots of a quadratic equation. It is given by x = [-b ± √(b^2 – 4ac)] / 2a.
2. How do I use the quadratic formula or 근의 공식?
To use the quadratic formula, you first need to ensure that your equation is in the standard form ax^2 + bx + c = 0. Then, you can simply substitute the values of a, b, and c into the formula to find the roots.
3. What is the discriminant in the quadratic formula or 근의 공식?
The discriminant in the quadratic formula is the expression inside the square root, b^2-4ac. It determines the nature of the roots. If the discriminant is positive, the quadratic equation has two real roots. If it is zero, the equation has one real root. If it is negative, the equation has two complex conjugate roots.
4. What is the degree of the quadratic equation?
The degree of the quadratic equation is two because it involves a variable raised to the power of two.
5. Can the quadratic formula be used for complex numbers?
Yes, the quadratic formula can be used for complex numbers. If the discriminant is negative, the roots will be complex conjugates.
In conclusion, the quadratic formula or 근의 공식 is a powerful mathematical tool that can be used in many applications, such as physics, engineering, economics, and finance. By understanding how to use this formula, you can solve complex problems and make informed decisions in various fields.
주제와 관련된 이미지 근의공식 짝수

근의공식 짝수 주제와 관련된 이미지 21개를 찾았습니다.


![중학 기본개념] 근의 공식, 짝수 근의 공식 중학 기본개념] 근의 공식, 짝수 근의 공식](https://t1.daumcdn.net/cfile/tistory/210B884055C0B6C21F)
![중학 기본개념] 근의 공식, 짝수 근의 공식 중학 기본개념] 근의 공식, 짝수 근의 공식](https://t1.daumcdn.net/cfile/tistory/2347504655C0B6AE24)

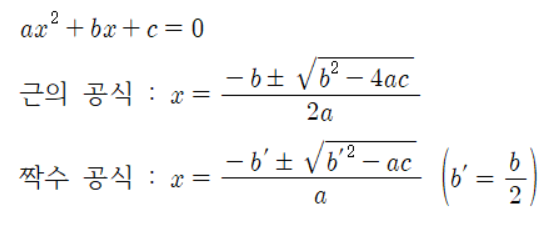
![중학 기본개념] 근의 공식, 짝수 근의 공식 중학 기본개념] 근의 공식, 짝수 근의 공식](https://t1.daumcdn.net/cfile/tistory/216F3D4155C0B6AC22)






![이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기) 이차방정식] 근의 공식 유도과정 (시험에 99% 출제되므로 필수 암기)](https://blog.kakaocdn.net/dn/b16TIv/btqEljBSogl/AskNAzMjpxr8NvnoGImOlK/img.png)
















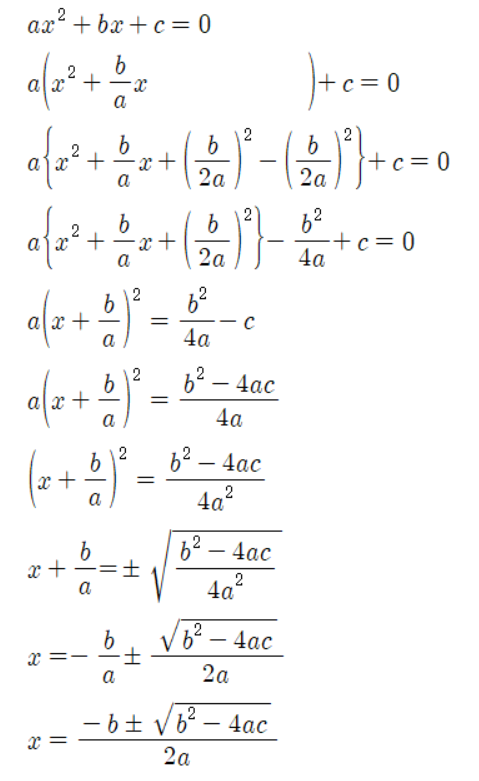
![수학짤] 짝수근의공식, 짝수판별식 설명 - YouTube 수학 공식 | 고등학교 > 거듭제곱근의 뜻과 성질 – Math Factory” style=”width:100%” title=”수학 공식 | 고등학교 > 거듭제곱근의 뜻과 성질 – MATH FACTORY”><figcaption>수학 공식 | 고등학교 > 거듭제곱근의 뜻과 성질 – Math Factory</figcaption></figure>
<figure><img decoding=](https://www.mathfactory.net/wp-content/uploads/%EC%A7%80%EC%88%98%EC%99%80-%EB%A1%9C%EA%B7%B8-%EA%B3%B5%EC%8B%9D-01.png)

![고등상 중요개념] 2-2. 이차방정식 #01탄 || 근의 공식 유도 - YouTube 고등상 중요개념] 2-2. 이차방정식 #01탄 || 근의 공식 유도 - Youtube](https://i.ytimg.com/vi/5QosFvl_NI0/mqdefault.jpg)





Article link: 근의공식 짝수.
주제에 대해 자세히 알아보기 근의공식 짝수.
- 근의 공식, 근의 공식 유도, 짝수 공식 – 수학방
- 짝수 근의 공식 (이차방정식 짝수 공식) – 모든 수학
- [중학 기본개념] 근의 공식, 짝수 근의 공식 – 부형식 수학 – 티스토리
- [5분 고등수학] 이차방정식의 근의공식 유도 (기본,짝수)
더보기: b1.brokengroundgame.com/krblog

